Docsity
Log inSign up
Docsity
Prepare for your exams
Prepare for your exams

Study with the several resources on Docsity

Earn points to download
Earn points to download

Earn points by helping other students or get them with a premium plan

Guidelines and tips
Guidelines and tips
Sell on Docsity
Sell on Docsity
Log inSign up

Prepare for your exams

Study with the several resources on Docsity

Find documents

Prepare for your exams with the study notes shared by other students like you on Docsity

Search Store documents

The best documents sold by students who completed their studies

Search through all study resources
Docsity AINEW

Summarize your documents, ask them questions, convert them into quizzes and concept maps

Explore questions

Clear up your doubts by reading the answers to questions asked by your fellow students

Earn points to download

Earn points by helping other students or get them with a premium plan

Share documents
download point icon20 Points

For each uploaded document

Answer questions
download point icon5 Points

For each given answer (max 1 per day)

All the ways to get free points
Get points immediately

Choose a premium plan with all the points you need

Study Opportunities

Choose your next study program

Get in touch with the best universities in the world. Search through thousands of universities and official partners

Community

Ask the community

Ask the community for help and clear up your study doubts

University Rankings

Discover the best universities in your country according to Docsity users

Free resources

Our save-the-student-ebooks!

Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors

From our blog

Exams and Study
Go to the blog

Calculus II Test 3 - MATH 211, Millersville University, Exams of Calculus

Millersville University of Pennsylvania (MU)Calculus

Millersville university's calculus ii (math 211) test 3, held on march 29, 2005, from 9:00am-9:50am. The test covers various concepts of calculus, including series convergence and divergence, sequences, and infinite series. Students are required to answer questions related to determining the tests for convergence or divergence of series and sequences, finding their limits or sums, and estimating the sums of infinite series.

Typology: Exams

Pre 2010

Uploaded on 08/19/2009

koofers-user-xq9
koofers-user-xq9 🇺🇸

10 documents

1 / 6

Toggle sidebar

This page cannot be seen from the preview

Don't miss anything!

bg1
Millersville University Name
Department of Mathematics
MATH 211, Calculus II , Test 3
March 29, 2005, 9:00AM-9:50AM
Please answer the following questions. Your answers will be evaluated on their correctness,
completeness, and use of mathematical concepts we have covered. Please show all work and
write out your work neatly. Answers without supporting work will receive no credit. The
point values of the problems are listed in parentheses.
1. (8 points each) Determine whether the following series converge or diverge. You must
clearly describe the tests for convergence or divergence used in each case. If a series
converges, find its sum.
(a)
∞
X
k=0 1
3k−4
7k
(b)
∞
X
k=0 e−k−e−k−1
pf3
pf4
pf5

Partial preview of the text

Download Calculus II Test 3 - MATH 211, Millersville University and more Exams Calculus in PDF only on Docsity!

Millersville University Name Department of Mathematics MATH 211, Calculus II , Test 3 March 29, 2005, 9:00AM-9:50AM

Please answer the following questions. Your answers will be evaluated on their correctness, completeness, and use of mathematical concepts we have covered. Please show all work and write out your work neatly. Answers without supporting work will receive no credit. The point values of the problems are listed in parentheses.

  1. (8 points each) Determine whether the following series converge or diverge. You must clearly describe the tests for convergence or divergence used in each case. If a series converges, find its sum.

(a)

∑^ ∞

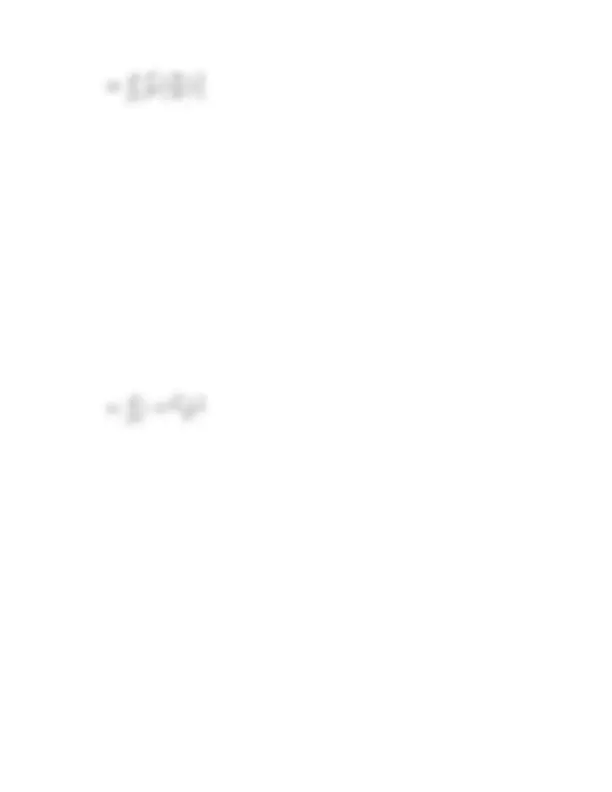
k=

( 1 3 k^

7 k

)

(b)

∑^ ∞ ( e−k^ − e−k−^1

)

  1. (8 points) Determine whether the following sequence converges or diverges. You must justify your answer to receive full credit for the problem. If the sequence converges, find its limit. ak = (−1)k+^

ln k k^2

  1. (10 points each) Determine whether the following series are divergent, conditionally convergent, or absolutely convergent. You must clearly describe the tests for conver- gence or divergence used in each case.

(a)

∑^ ∞ (−3)k k^24 k

(d)

∑^ ∞

k=

k^2 + 3k + 2 k^2 + 2k + 1

(e)

∑^ ∞ (−1)k^

k^2 + 1 k^3

  1. (8 points each) Consider the following sequence.

ak =

5 k − 2 3 k + 1

(a) Determine whether the sequence is monotone increasing or monotone decreasing. You must justify your answer.

(b) Determine a bound for the sequence.