












































Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Edge in 1D, Derivatives and Noise, Edges in 2D, Visualizing Derivatives, Derivative of Gaussian Filter, Derivative of Gaussian in 2D, Sobel Operators, Image Gradient, Computing Gradient, Thresholding the Gradient, Canny Edge Detector, Canny: Non-Maxima Suppresion, Canny: Hysteresis, Difference of Gaussians, Log, Dog, Zero Crossing Edge Detection, Scale Space, Human Edge Detection, Greg Shakhnarovich, Lecture Slides, Introduction to Computer Vision, Computer Science, Toyota Technological Institut
Typology: Lecture notes
1 / 57

This page cannot be seen from the preview
Don't miss anything!


















































Greg Shakhnarovich
April 15, 2010
Gaussians: x
p(x)
Gaussian blurring
Filter separability; integral image (^) A
Let’s start with 1D problem
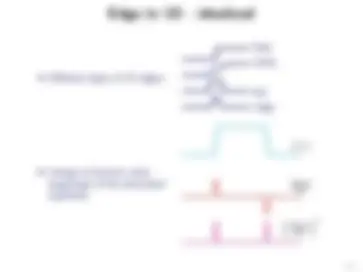
Different types of 1D edges:
step ramp
bar ridge
Different types of 1D edges:
step ramp
bar ridge
change in function value: magnitude of the derivative!
f (x)
∂f (x) ∂x
Different types of 1D edges:
step ramp
bar ridge
change in function value: magnitude of the derivative! (squared)
f (x)
∂f (x) ∂x
( (^) ∂f (x) ∂x
x − 1 x^ x + 1
I(x)
x − 1 x^ x + 1
I(x) I(x − 1)
I(x + 1)
x − 1 x^ x + 1
I(x) I(x − 1)
I(x + 1) Ix(x)^ ,^
∂x = (^) ∆limx→ 0 I(x + ∆x) − I(x) ∆x ≈ I(x + 1) − I(x) ≈ I(x + 1) − I(x − 1)
x − 1 x^ x + 1
I(x) I(x − 1)
I(x + 1) Ix(x)^ ,^
∂x = (^) ∆limx→ 0 I(x + ∆x) − I(x) ∆x ≈ I(x + 1) − I(x) ≈ I(x + 1) − I(x − 1)
Can we compute the derivative by convolution?
x − 1 x^ x + 1
I(x) I(x − 1)
I(x + 1) Ix(x)^ ,^
∂x = (^) ∆limx→ 0 I(x + ∆x) − I(x) ∆x ≈ I(x + 1) − I(x) ≈ I(x + 1) − I(x − 1)
Can we compute the derivative by convolution? Yes: filter mask Dx =
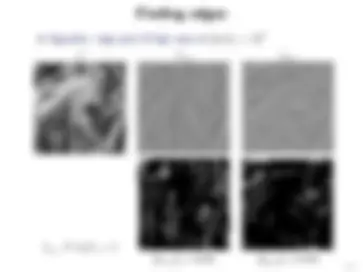
Barbara 1D profile:
x − 1 x^ x + 1
I(x) I(x − 1)
I(x + 1) Ix(x)^ ,^
∂x = (^) ∆limx→ 0 I(x + ∆x) − I(x) ∆x ≈ I(x + 1) − I(x) ≈ I(x + 1) − I(x − 1)
Can we compute the derivative by convolution? Yes: filter mask Dx =
Barbara 1D profile:
Ix = I ∗ Dx
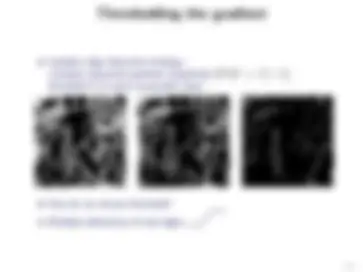
Smoothing the signal and then taking the derivative:
Smoothing the signal and then taking the derivative:
I ∗ Gx,σ