Download De Broglie Waves, Uncertainty, and Atoms - Lecture Slides | PHY 1161 and more Exams Physics in PDF only on Docsity!
Physics 1161: Lecture 23, Slide 1
De Broglie Waves, Uncertainty, and Atoms
- Today’s Lecture will cover textbook sections 30-5 – 30-
Physics 1161: Lecture 23 Final
Exam
Physics 1161: Lecture 23, Slide 2
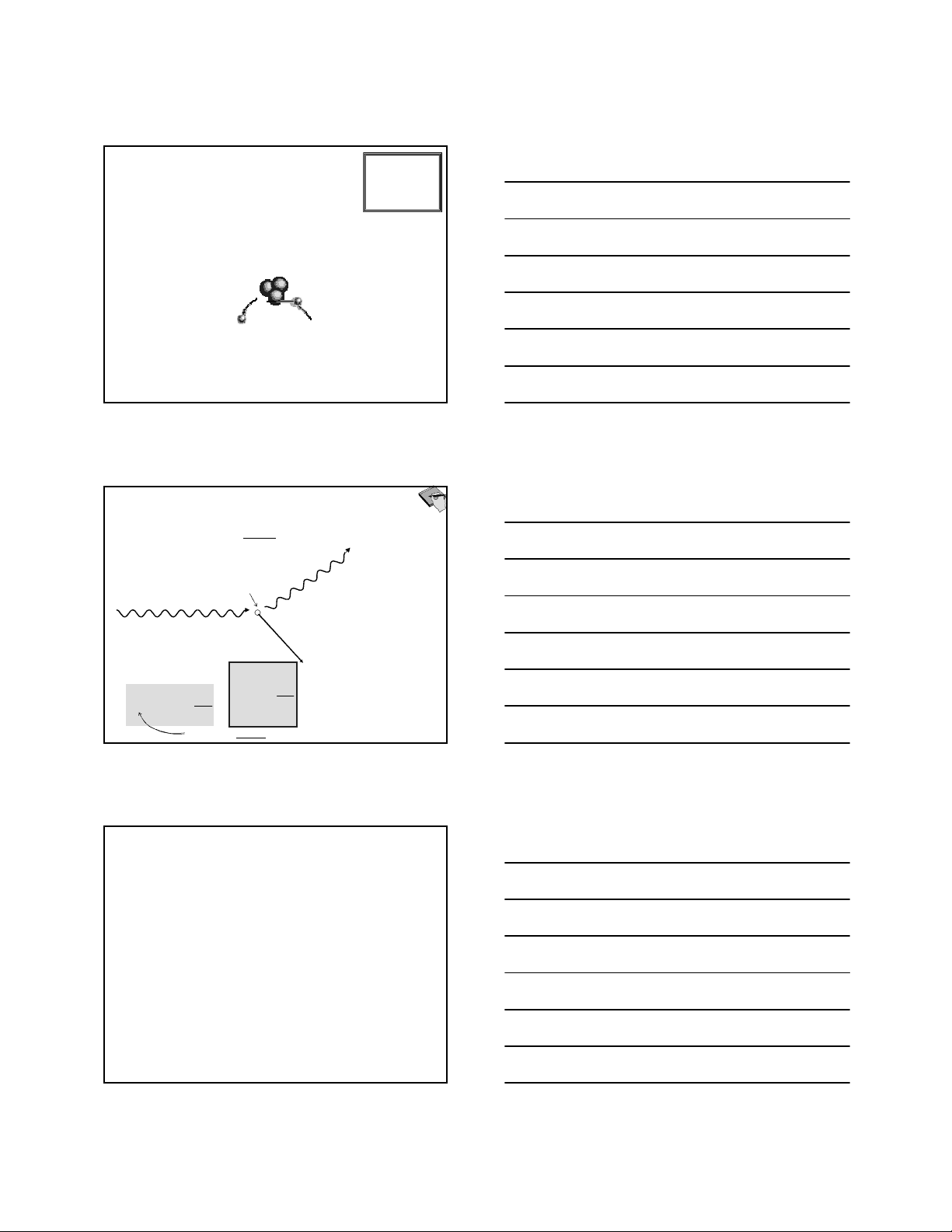
Outgoing photon has momentum p′′′′ and wavelength λλλλ′′′′
Recoil electron carries some momentum and KE
Incoming photon has momentum, p, and wavelength λλλλ
This experiment really shows photon momentum!
Electron at rest
Compton Scattering
Pincoming photon + 0 = Poutgoing photon + Pelectron
hc
E = hf =
h
p =
Energy of a photon
Physics 1161: Lecture 23, Slide 3
ACT: Photon Collisions
Photons with equal energy and momentum hit both
sides of the plate. The photon from the left sticks
to the plate, the photon from the right bounces off
the plate. What is the direction of the net impulse
on the plate?
1) Left 2) Right 3) Zero
Physics 1161: Lecture 23, Slide 4
Black side (absorbs)
Shiny side (reflects)
Incident photons
Radiometer
Preflight 23.
Photon A strikes a black surface and is absorbed. Photon B strikes a shiny surface and is reflected back. Which photon imparts more momentum to the surface?
Photon A Photon B
Physics 1161: Lecture 23, Slide 5
λ
h p =
So far only for photons have wavelength, but De Broglie postulated that it holds for any object with momentum- an electron, a nucleus, an atom, a baseball,…...
Explains why we can see interference and diffraction for material particles like electrons!!
De Broglie Waves
p
h λ =
Physics 1161: Lecture 23, Slide 6
Which baseball has the longest De Broglie wavelength?
(1) A fastball (100 mph) (2) A knuckleball (60 mph) (3) Neither - only curveballs have a wavelength
Preflight 23.
Physics 1161: Lecture 23, Slide 10
ACT: De Broglie
Compare the wavelength of a bowling ball with the wavelength of a golf ball, if each has 10 Joules of kinetic energy.
(1) λbowling > λgolf
(2) λbowling = λgolf
(3) λbowling < λgolf
Physics 1161: Lecture 23, Slide 11
Rough idea: if we know momentum very precisely, we lose knowledge of location, and vice versa.
If we know the momentum p, then we know the wavelength λ, and that means we’re not sure where along the wave the particle is actually located!
λλ λλ
y
Heisenberg Uncertainty Principle
h
∆py ∆ y≥
Physics 1161: Lecture 23, Slide 12
Number of electrons arriving at screen sin θ =
λ w
⇒ w =
λ sin θ
screen
w
x
y
pθθ θθ
p θ ∆py = p sinθθθθ θθθ
Heisenberg Test
∆y = w = λ/sinθ
h
∆py ∆ y≥
electron beam
Physics 1161: Lecture 23, Slide 13
Electron entered slit with momentum along x direction and no momentum in the y direction. When it is diffracted it acquires a py which can be as big as h/w.
The “Uncertainty in py” is ∆∆∆∆py≈≈≈≈ h/w. An electron passed through the slit somewhere along the y direction. The “Uncertainty in y” is ∆∆∆∆y ≈≈≈≈ w.
Electron diffraction
electron beam
screen
Number of electrons arriving at screen
w
x
y (^) p (^) y ⋅ w = h
py
∴ ∆py ⋅ ∆y ≈ h
Physics 1161: Lecture 23, Slide 14
electron beam
screen
Number of electrons arriving at screen
w
x
y
py
∴ ∆py ⋅ ∆y ≈ h
If we make the slit narrower (decrease w=∆∆∆∆y) the diffraction peak gets broader (∆∆∆∆py increases).
“If we know location very precisely, we lose knowledge of momentum, and vice versa.”
Remember earlier we saw that a particle whose momentum (and therefore wavelength) is known precisely is very uncertain in position.
Physics 1161: Lecture 23, Slide 15
to be precise... ∆p^ y∆y^ ≥^
h 2 π
Of course if we try to locate the position of the particle along the x axis to ∆∆∆∆x we will not know its x component of momentum better than ∆px, where
∆p (^) x∆x ≥
h 2 π and the same for z.
Preflight 23.
According to the H.U.P., if we know the x-position of a particle, we can not know its: (1) Y-position (2) x-momentum (3) y-momentum (4) Energy
Physics 1161: Lecture 23, Slide 19
Photons bouncing off shiny side and sticking to black side. Shiny side gets more momentum so it should rotate with the black side leading
Ideal Radiometer
Physics 1161: Lecture 23, Slide 20
Our Radiometer
Black side is hotter:gas molecules bounce off it with more momentum than on shiny side-this is a bigger effect than the photon momentum
Physics 1161: Lecture 23, Slide 21
Recap
- Photons carry momentum p=h/λ
- Everything has wavelength λ=h/p
- Uncertainty Principle ∆p∆x > h/(2π)
- Atom
- Positive nucleus 10-15^ m
- Electrons “orbit” 10-10^ m
- Classical E+M doesn’t give stable orbit
- Need Quantum Mechanics!
Physics 1161: Lecture 23, Slide 22
See you Wednesday!
- Read Textbook Sections 30-5 – 30-
