
























Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
A lecture note from csci 533: artificial intelligence course at texas a&m university - commerce, fall 2007. The lecture covers constraint satisfaction problems (csps), their formal representation, varieties, and search methods such as backtracking search and constraint propagation. The document also discusses the concept of constraint graphs and their role in solving csps.
Typology: Assignments
1 / 42

This page cannot be seen from the preview
Don't miss anything!



































Derek Harter – Texas A&M University - Commerce Many slides over the course adapted from Srini Narayanan, Dan Klein, Stuart Russell or Andrew Moore
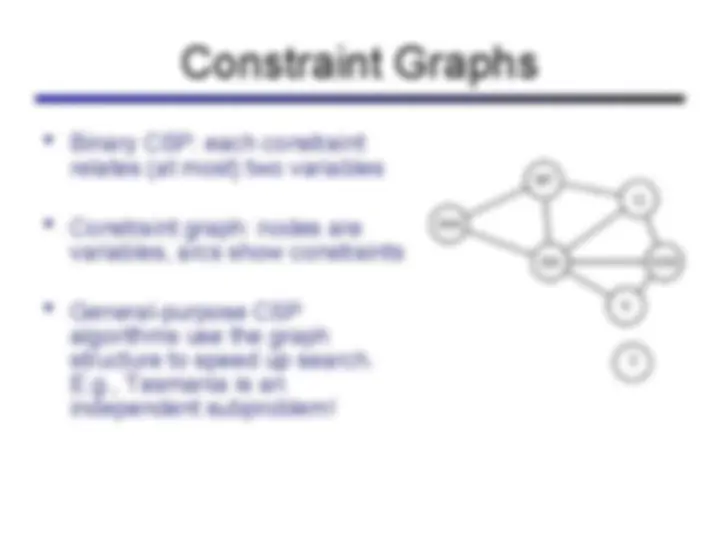
Constraint Satisfaction Problems
(^) State is a “black box”: any old data structure (^) Goal test: any function over states (^) Successors: any map from states to sets of states
i with values from a
(^) Goal test is a set of constraints specifying allowable combinations of values for subsets of variables
(^) E.g., Boolean CSPs, including Boolean satisfiability (NP-complete)
(^) E.g., job scheduling, variables are start/end times for each job (^) Need a constraint language , e.g., StartJob 1 + 5 < StartJob 3 (^) Linear constraints solvable, nonlinear undecidable
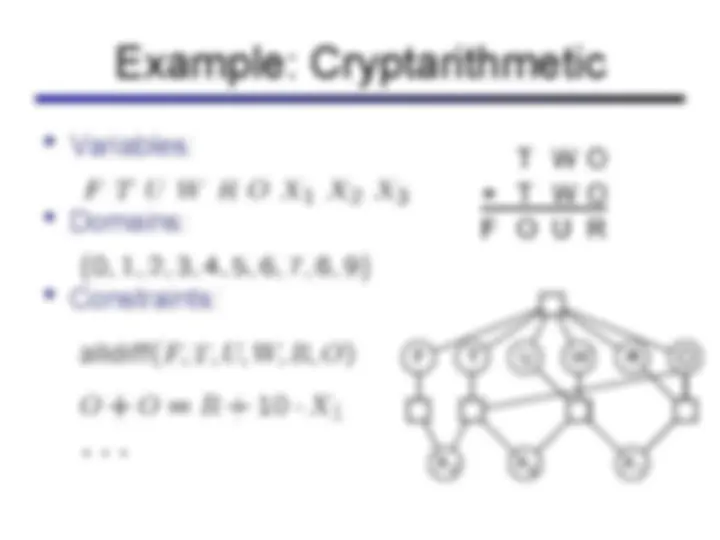
(^) Unary constraints involve a single variable (equiv. to shrinking domains): (^) Binary constraints involve pairs of variables: (^) Higher-order constraints involve 3 or more variables: e.g., cryptarithmetic column constraints
(^) E.g., red is better than green (^) Often representable by a cost for each variable assignment (^) Gives constrained optimization problems (^) (We’ll ignore these until we get to Bayes’ nets)
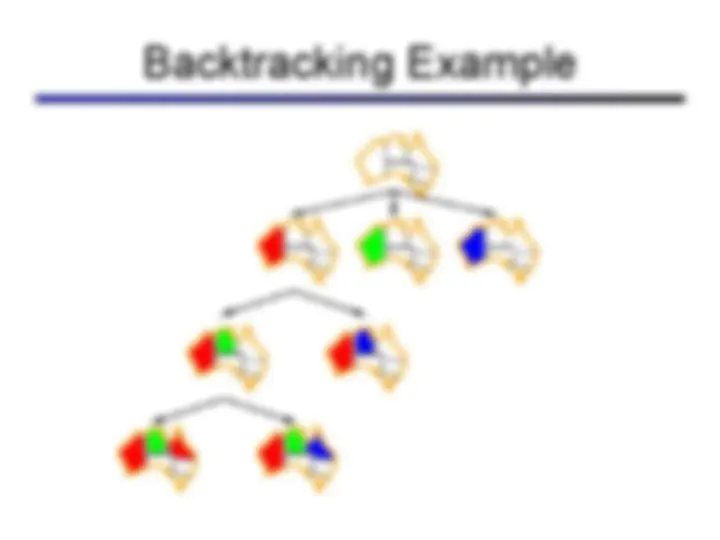
(^) Variable assignments are commutative (^) I.e., [WA = red then NT = green] same as [NT = green then WA = red] (^) Only need to consider assignments to a single variable at each step (^) How many leaves are there?
(^) I.e. consider only values which do not conflict previous assignments (^) Might have to do some computation to figure out whether a value is ok