Computational Complexity: Growth Rates and Orders of Magnitude, Lecture notes of Data Structures and Algorithms

Download Computational Complexity: Growth Rates and Orders of Magnitude and more Lecture notes Data Structures and Algorithms in PDF only on Docsity!

Computational Complexity,

Orders of Magnitude

n Rosen Ch. 3.2: Growth of Functions

n Rosen Ch. 3.3: Complexity of Algorithms

n Prichard Ch. 10.1: Efficiency of Algorithms

CS200 - Complexity 1

Algorithm and Computational

Complexity

n An algorithm is a finite sequence of precise

instructions for performing a computation for

solving a problem.

n Computational complexity measures the

processing time and computer memory

required by the algorithm to solve problems

of a particular problem size.

CS200 - Complexity 2

Units of time

n 1 microsecond?

n 1 machine instruction?

n # of code fragments that take constant time?

Units of time

n 1 microsecond?

no, too specific and machine dependent

n 1 machine instruction?

no, still too specific and machine dependent

n # of code fragments that take constant time?

yes

unit of space

n bit?

very detailed but sometimes necessary

n int?

nicer, but dangerous: we can code a whole

program or array (or disk) in one arbitrary int, so

we have to be careful with space analysis (take

value ranges into account when needed). Better

to think in terms of machine words

i.e. fixed size, 64 bit words

8

Worst-Case Analysis

n Worst case running time.

n A bound on largest possible running time of algorithm on

inputs of size n.

q Generally captures efficiency in practice, but can be

an overestimate.

n Same for worst case space complexity

Measuring the efficiency of algorithms

n We have two algorithms: alg1 and alg2 that

solve the same problem. Our application

needs a fast running time.

n How do we choose between the algorithms?

CS200 - Complexity 10

Efficiency of algorithms

n Implement the two algorithms in Java and

compare their running times?

n Issues with this approach:

q How are the algorithms coded? We want to compare the algorithms, not the implementations. q What computer should we use? Choice of operations could favor one implementation over another. q What data should we use? Choice of data could favor one algorithm over another CS200 - Complexity 11

Example: array copy

n Copying an array with n elements requires

___ invocations of copy operations

How many steps?

How many instructions?

How many micro seconds?

CS200 - Complexity 13

Example: linear Search

n What is the maximum number of steps linSearch takes?

what’s a step here?

for an Array of size 32?

for an Array of size n?

CS200 - Complexity 14 private int linSearch(int k){ for(int i = 0; i<A.length; i++ ){ if(A[i]==k) return i; } return -1; }

Growth rates A. Algorithm A requires n 2 / 2 steps to solve a problem of size n B. Algorithm B requires 5n+10 steps to solve a problem of size n n Which one would you choose? CS200 - Complexity 16

Growth rates n When we increase the size of input n , how the execution time grows for these algorithms? n We don’t care about small input sizes n 1 2 3 4 5 6 7 8 n 2 / 2 .5 2 4.5 8 12.5 18 24.5 32 5n+10 15 20 25 30 35 40 45 50 n 50 100 1,000 10,000 100, n 2 / 2 1250 5,000 500,000 50,000,000 5,000,000, 5n+10 260 510 5,010 50,010 500, CS200 - Complexity 17

Growth rates n Algorithm A requires n 2 / 2 +1 operations to solve a problem of size n n Algorithm B requires 5n + 10 operations to solve a problem of size n n For large enough problem size algorithm B is more efficient n Important to know how quickly an algorithm’s execution time grows as a function of program size q We focus on the growth rate: n Algorithm A requires time proportional to n^2 n Algorithm B requires time proportional to n n B’s time requirement grows more slowly than A’s time requirement (for large n) CS200 - Complexity 19

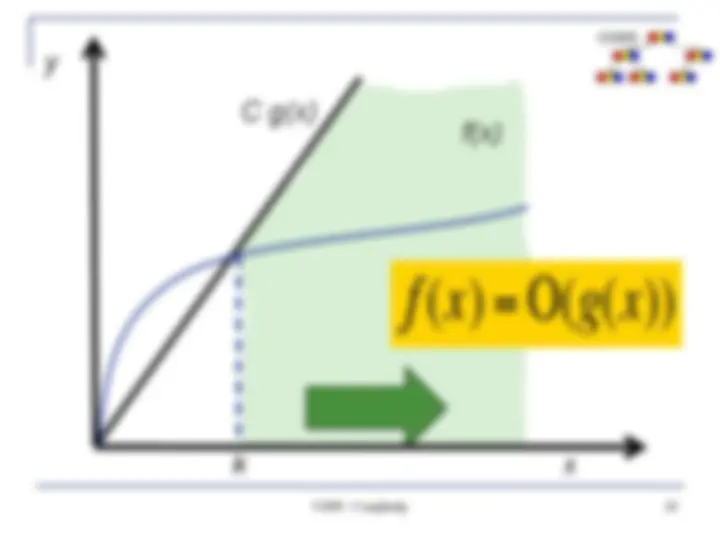
Order of magnitude analysis n Big O notation: A function f(x) is O(g(x)) if there exist two positive constants, c and k, such that f(x) ≤ c*g(x) ∀ x > k CS200 - Complexity 20