



Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
este documento contiene temas de preparación para las pruebas nacionales
Typology: Summaries
1 / 5

This page cannot be seen from the preview
Don't miss anything!




1. Introducción Dominio Matemático: Clave para el ICFES y la Vida En esta sesión, nos enfocamos en la importancia fundamental de dominar los conceptos matemáticos. Esto no solo es una herramienta esencial para superar la prueba ICFES, sino también una habilidad indispensable para enfrentar los desafíos de la vida cotidiana. Exploramos las competencias matemáticas específicas que el ICFES evalúa, identificando los conceptos clave que los estudiantes deben dominar. Además, nos sumergimos en la contextualización de problemas, aprendiendo a aplicar las matemáticas en una variedad de situaciones reales, desarrollando así la capacidad de resolver problemas de manera efectiva y práctica. Analizamos en detalle la estructura de la prueba ICFES, desglosando el peso porcentual de cada competencia evaluada, lo que permite a los estudiantes comprender mejor el formato del examen y enfocar sus esfuerzos de preparación. A través de la discusión de contextos y situaciones problema, buscamos fortalecer la capacidad de los estudiantes para abordar diferentes desafíos matemáticos con confianza y precisión (Adjunto el documento analizado) 2. Conjuntos Numéricos Teoría: Los números se agrupan en diferentes conjuntos según sus propiedades:
Ciencias Básicas
3. Números Enteros Teoría: Los números enteros incluyen positivos, negativos y el cero. Operaciones:
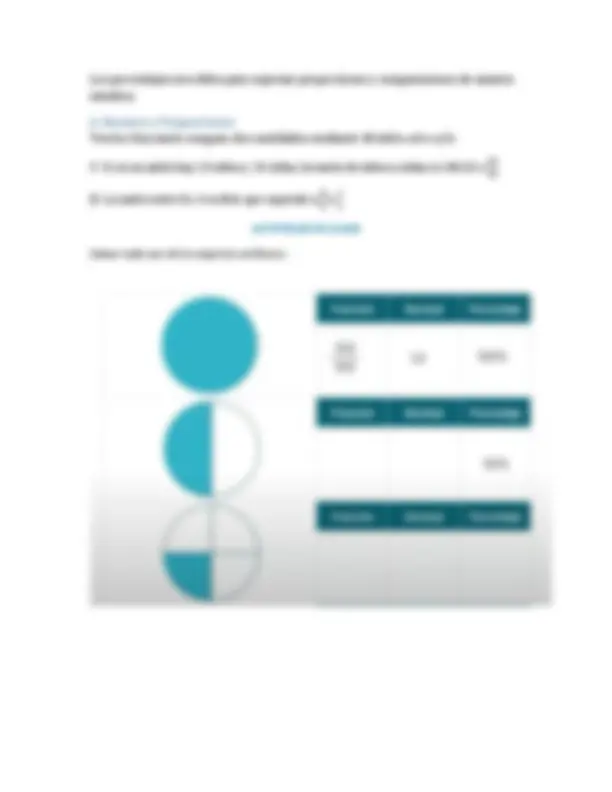
Los porcentajes son útiles para expresar proporciones y comparaciones de manera intuitiva.
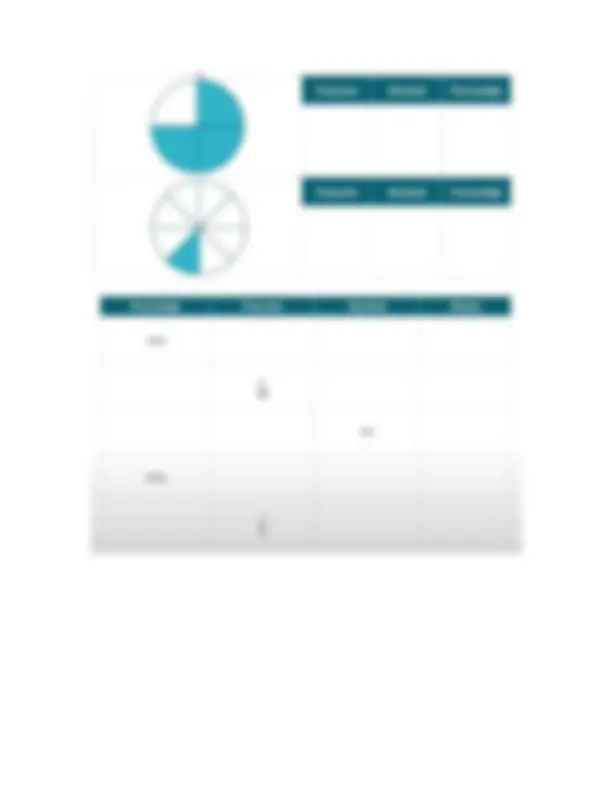
6. Razones y Proporciones Teoría: Una razón compara dos cantidades mediante división: a:b o a/b. Si en un salón hay 10 niños y 15 niñas, la razón de niños a niñas es 10:15 o 10 15 La razón entre 8 y 4 es 8:4 , que equivale a 8 4 o 1 2 ACTIVIDAD EN CLASE Llenar cada uno de los espacios en blanco.