Download Chapter 3: The basic concepts of probability and more Study notes Probability and Statistics in PDF only on Docsity!
Chapter 3: The basic concepts of probability
Experiment: a measurement process that produces quantifiable results (e.g. throwing two dice, dealing cards, at poker, measuring heights of people, recording proton-proton collisions)
Outcome: a single result from a measurement (e.g. the numbers shown on the two dice)
Sample space: the set of all possible outcomes from an experiment (e.g. the set of all possible five-card hands)
The number of all possible outcomes may be (a) finite (e.g. all possible outcomes from throwing a single die; all possible 5-card poker hands) (b) countably infinite (e.g. number of proton-proton events to be made before a Higgs boson event is observed) or (c) constitute a continuum ( e.g. heights of people)
In case (a), the sample space is said to be finite in cases (a) and (b), the sample space is said to be discrete in case (c), the sample space is said to be continuous
In this chapter we consider discrete, mainly finite, sample spaces
An event is any subset of a sample set (including the empty set, and the whole set)
Two events that have no outcome in common are called mutually exclusive events.
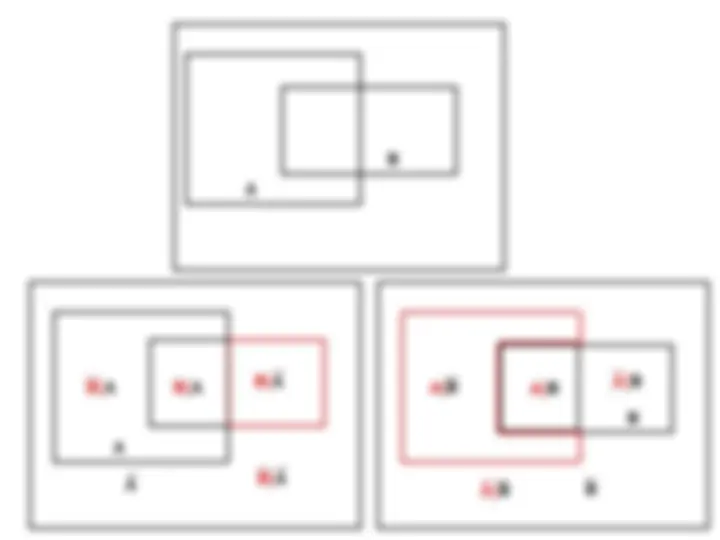
In discussing discrete sample spaces, it is useful to use Venn diagrams and basic set-
theory. Therefore we will refer to the union (A U B) , intersection, (A โฉ B) and
complement (แพน) of events A and B. We will also use set-theory relations such as
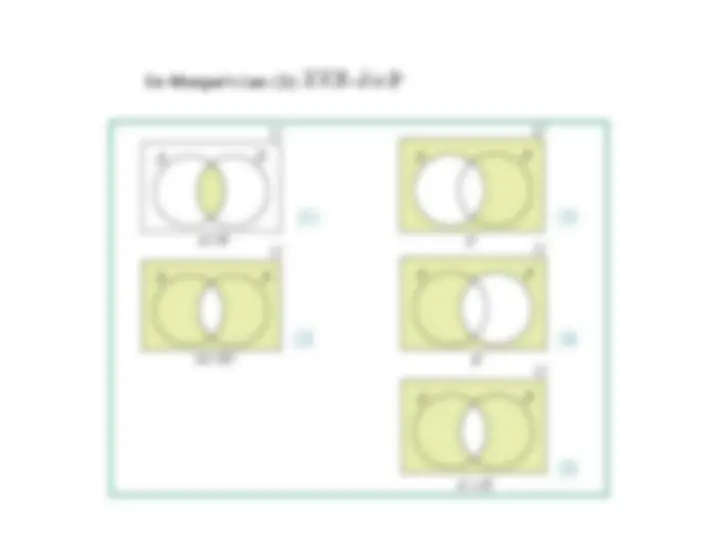
A U B = A โฉ B (Such relations are often proved using Venn diagrams)
This is also called De Morganโs law, another half of De Moganโs law is:
๐ดโ๐ต=๐ดโ๐ต
Some terminology used in card game
Flush: A flush is a hand of playing cards where all cards are of the same suit.
Straight:
Three of a kind:
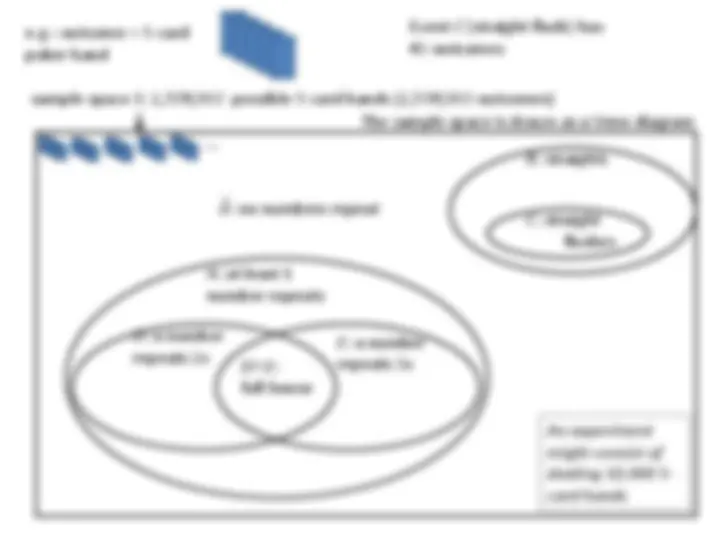
e.g.: outcome = 5-card poker hand
sample space S : 2,598,960 possible 5-card hands (2,598,960 outcomes)
A: at least 1 number repeats
๐ด: no numbers repeat
B : straights
C : straight flushes
D : a number repeats 2x
E : a number DโฉE :^ repeats 3x full house
Event C (straight flush) has 40 outcomes
The sample space is drawn as a Venn diagram
An experiment might consist of dealing 10,000 5- card hands
De Morganโs Law (1): ๐ด โฉ ๐ต=๐ด โช ๐ตฬ
Example: U=(3,4,2,8,9,10,27,23,14)
A=(2,4,8) B=(3,4,8,27)
๐ด=(3,9,10,27,23,14) ๐ต =(2,9,10,23,14) ๐ด โช ๐ต=(2,3,4,8,27) ๐ด โฉ ๐ต=(4,8) ๐ด โ ๐ต=(2) ๐ด โช ๐ต=(9,10,23,14) ๐ด โฉ ๐ต=(3,9,10,27,23,14,2)
Counting principles:
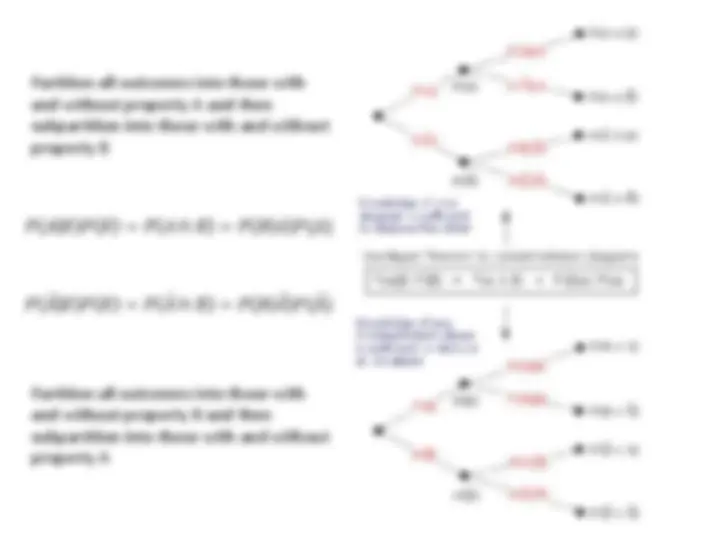
The addition principle: If there are n 1 outcomes in event A 1 , n 2 outcomes in event A 2 , โฆ nk outcomes in event Ak
and the events A 1 , A 2 , โฆ Ak are mutually distinct (share no outcomes in common),
then the total number of outcomes in A 1 U A 2 U โฆ U Ak is n 1 + n 2 + โฆ + nk
A single outcome may consist of several distinct parts (e.g. an arrangement of 7
objects; throwing a red and a green die). Such outcomes are said to be composite
The multiplication principle: If a composite outcome can be described by a procedure that can be broken into k successive (ordered) stages such that there are n 1 outcomes in stage 1, n 2 outcomes in event 2, โฆ nk outcomes in event k
and if the number of outcomes in each stage is independent of the choices in previous
stages and if the composite outcomes are all distinct
then the number of possible composite outcomes is n 1 ยท n 2 ยท โฆ ยท nk
e.g. suppose the composite outcomes of the trio (M.P,C) of class values for cars, where M denotes the mileage class (M 1 , M 2 , or M 3 ) P denotes the price class (P 1 , or P 2 ) C denotes the operating cost class (C 1 , C 2 , or C 3 )
The outcome is clearly written as a 3-stage value There are 3 outcomes in class M, 2 in class P and 3 in class C The number of outcomes in class P does not depend on the choice made for M, etc Then there will be 3 ยท 2 ยท 3 = 18 distinct composite outcomes for car classification.
e.g. an outcome of an experiment consists of an operator using a machine to test a type of sample. If there are 4 different operators, 3 different machines, and 8 different types of samples, how many experimental outcomes are possible?
Note: the conditions of the multiplication principle must be strictly adhered to for it to work.
e.g. the number of distinct outcomes obtained from throwing two identical six-sided dice cannot be obtained by considering this as a two stage process (the result from the first die and then the result from the second โ since the outcomes from the two stages are not distinct. There are not 36 possible outcomes from throwing two identical six-sided dice; there are only 21 distinct outcomes.
e.g. the number of distinct outcomes obtained from throwing a red six-sided dice and a green six-sided dice can be determined by the multiplication principle. There are 36 possible outcomes in this case.
e.g. the number of 5-card poker hands comprised of a full house can be computed using the multiplication principle. A full house can be considered a two-stage hand, the first stage being the pair, the second stage being the three-of-a-kind. Thus the number of possible full house hands = (the number of pairs) x (the number of threes-of-a-kind)
e.g. the number of 5-card poker hands comprised of a full house that do not contain the 10 โs as the three-of-a-kind cannot be computed using the multiplication principle since the number of choices for the three-of-a-kind depends on whether-or-not the pair consists of 10โs
r โ permutations Given n distinct objects, how many ways are there to arrange exactly r of the objects? An arrangement is a sequence (ordered stages) of successive objects. An arrangement can be thought of as putting objects in slots. There is a distinct first slot, second slot, โฆ., kโ th slot, and so on. Putting object A in the first slot and B in the second is a distinct outcome from putting B in the first and A in the second. The number of possible choices for slot k +1 does not depend on what choice is used for slot k. Therefore the multiplication principle can be used. Thus the number of ways to arrange r of the n distinct objects is ๐๐๐ = ๐^ ๐ โ 1^ ๐ โ 2 โฆ. ๐ โ ๐ + 1 Multiplying and dividing by ( nโr )!, this can be written
๐๐๐ =^
๐ ๐โ1 ๐โ2 โฆ. ๐โ๐+1 ๐โ๐! ๐โ๐! =^
๐! ๐โ๐! Theorem 3.2 The number of r โ permutations of n distinct objects (that is the number of ways to arrange exactly r objects out of a set of n distinct objects) is
๐๐๐ =^
๐! ๐โ๐!
Note:
The number of ways to arrange all n objects is (^) ๐๐๐ = ๐! (as 0! โก1)
The number of ways to arrange zero of the n objects is (^) ๐๐ 0 = ๐!๐! = 1
Yang Hui in 1305
Pascal in 1655
Tartaglia in 1600โs
