










Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
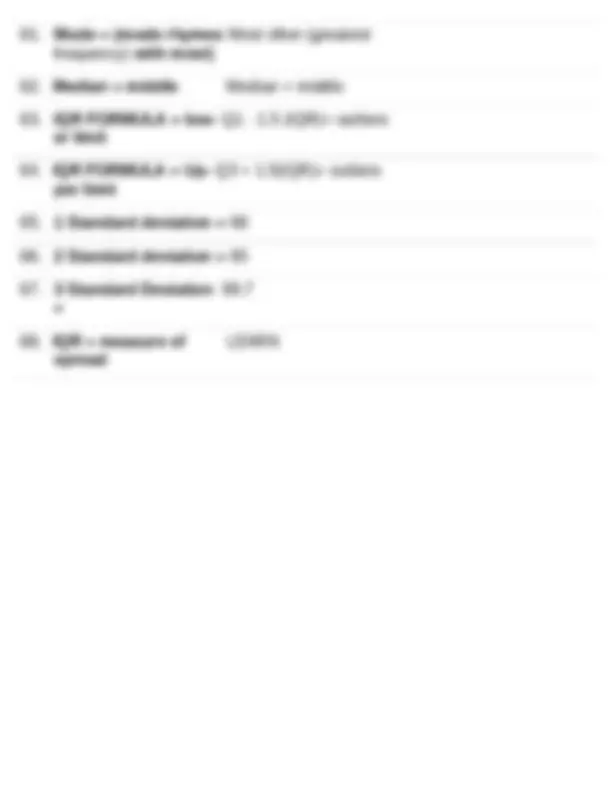
An overview of various types of numbers and data in mathematics and statistics, including integers, rational numbers, real numbers, discrete data, and continuous data. It explains the properties and characteristics of each type and provides examples. The document also covers related concepts such as sets, intervals, mean and median, and measures of spread.
Typology: Exams
1 / 18

This page cannot be seen from the preview
Don't miss anything!











In math, you may be asked to "evaluate an expression."--what does that mean?
listed in both of the sets.
Does ____ effect _______?
20)