Download Automatic Controls Systems and Mechatronics - Control Systems | ME 478 and more Study notes Control Systems in PDF only on Docsity!
© Dr. Seeler Department of Mechanical Engineering Fall 2004 Lafayette College
ME 478: Automatic Controls Systems and Mechatronics
Alternating Current, Phasors, Complex Impedance, and Three Phase Current
INTRODUCTION
Alternating current (AC) is driven by sinusoidal voltages. Analysis of AC circuits considers only the steady-state response, not the transient response. Since AC input voltage is sinusoidal and we are interested in the circuit’s steady-state response, we can use the tools we developed in ME 352 for frequency response. Recall from ME 352 that the steady-state response of a linear system to a sinusoidal input will be sinusoidal at the same frequency as the input but, possibly, shifted in time. The amplitude of the output sinusoid is the product of the amplitude of the input sinusoid and the magnitude of the transfer function evaluated by substituting for s the imaginary number j times the input frequency, s = jω.
Block Diagram of the Steady-State Response of a Linear System to a Sinusoidal Input
In AC circuits, the frequency is generally fixed at 60 Hz or 377 rad sec
. We will not be
concerned with the response of a system over a range of frequencies, just at one frequency. Further, the input sinusoid is always voltage and always assumed to have zero phase shift. Consequently, the frequency response relationship can be fully described by the amplitude of the
input, A, and the amplitude and phase shift of the output, A G ( jω) and φ. A quantity with a
magnitude and direction is a vector. We will review the mathematics needed to work with vectors in a complex plane. We will then introduce a vector representation tailored to AC circuit analysis. “Phasors” are similar to the vectors we worked with in ME 352, but rather than using the amplitude of the sinusoid as the magnitude of the vector, the magnitude of a phasor is the root mean square (RMS) or “effective” amplitude of the sinusoid.
Three phase current, widely used in industry, will be presented in the time domain and then represented using phasors. Analysis of AC circuits is performed using complex impedances based on the frequency response equation. The complex impedance method lends itself to graphical vector construction. Finally, we will investigate power AC systems.
Review of Complex Exponentials Euler’s Sine and Cosine Formulae
Before we begin working with sinusoidally varying voltages and currents, we will review prerequisite material from ME 352. Recall that Euler discovered that a complex exponential ejΘ is a unit vector in a complex plane:
e jΘ^ = cos Θ + jsin Θ
Expressed graphically:
Complex Exponential Unit Vector
The projection of a complex exponential unit vector ejΘ^ onto the real axis yields the cosine of the angle Θ and the projection onto the imaginary axis yields the imaginary unit vector j times the sine of the angle Θ. The projections of the complex exponential unit vector onto the real and imaginary axes are expressed in Mathcad and other engineering software as scalar functions:
( ) (^ ) Re e jΘ^ = cos Θ and ( ) ( Im e j^ sin e j )
Note that the function Im(ejΘ) yields the magnitude of the projection onto the imaginary axis as scalar, not an imaginary number.
Euler’s sine and cosine formulae also yield sin(Θ) and cos(Θ):
e j^ e j cos 2
Θ = and ( )
e j^ ej sin 2 j
Euler’s cosine and sine formulae expressed graphically as vector constructions:
We will apply the input(t) = A sin(ωt) to the transfer function. The Laplace transform of the input is:
A
A sin( t) s
ω ω =
L
Multiplying the transfer function G(s) by the Laplace transform of the input to obtain the Laplace transform of the output yields:
2 2
A 1
Input(s)G(s) Output(s) s s 2
⎛ ω ⎞⎛ ⎞ = (^) ⎜ ⎟⎜ ⎟= ⎝ + ω^ ⎠⎝ + ⎠
It is essential to remember that frequency response is the steady-state response of the system to the sinusoidal input. The frequency ω is a constant. We need to perform the inverse Laplace transform on Output(s) to return to the time domain and then take the limit as t → ∞.
Output(s) is not in the Laplace transform table, so we will need to perform partial fraction expansion to produce terms which are in the table. Normally, we would keep the denominator
factor because sine and cosine are in Laplace transform tables. However, in this case, we will factor the denominator into the product of first order factors for a reason which will be apparent later in the derivation. The partial fraction expansion is:
s 2 + ω^2
1 2
A 1 A 1
Output(s) s s 2 s j s j s
B B C
s j s j s 2
⎛ ω^ ⎞ ⎛ ⎞ ⎛^ ω ⎞⎛ ⎞ = (^) ⎜ ⎟ ⎜ ⎟ = ⎜⎜ ⎟⎟⎜ ⎟ ⎝ + ω^ ⎠ ⎝ +^ ⎠ (^) ⎝ + ω^ − ω^ ⎠⎝ + ⎠
⎝ + ω^ ⎠ ⎝ − ω^ ⎠ ⎝^ + ⎠
Determine the numerator constants B 1 , B 2 , and C by multiplying both sides by the denominator of the corresponding term, canceling identical factors, and evaluating using the pole of that term.
Constant B 1 :
A 1 B B C
s j s j s j s j s j s j s 2 s j s j s 2
⎛ (^) ω ⎞ (^) ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎜ ⎟⎟ (^) ⎜ ⎟ + ω =^ ⎜ ⎟ + ω +^ ⎜ ⎟ + ω +^ ⎜ ⎟ + ω ⎝ + ω^ − ω^ ⎠⎝^ +^ ⎠^ ⎝^ + ω^ ⎠^ ⎝^ − ω^ ⎠ ⎝^ + ⎠
1 2 (^ )^ (^ )
A 1 B C
B s j s s j s 2 s j s 2
⎛ (^) ω ⎞ (^) ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎜ ⎟⎟ (^) ⎜ ⎟ =^ +^ ⎜ ⎟ + ω +⎜ ⎟ j ⎝ − ω^ ⎠⎝^ +^ ⎠^ ⎝^ − ω^ ⎠ ⎝^ + ⎠
1 2 (^ )^ (^ )
s j s^ j s^ j
A 1 B C
B s j s j s j s (^2) =− ω s j (^) =− ω s (^2) =− ω
⎛ (^) ω ⎞ (^) ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎜ ⎟⎟ (^) ⎜ ⎟ =^ +^ ⎜ ⎟ + ω^ +^ ⎜ ⎟ + ω ⎝ − ω^ ⎠⎝^ +^ ⎠^ ⎝^ − ω^ ⎠ ⎝^ + ⎠
1 2 (^ )^ (^ )
A 1 B C
B j j j j j 2 j j s 2
⎛ (^) ω ⎞⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎜⎜ ⎟⎜⎟ ⎟ =^ +^ ⎜ ⎟ − ω + ω +^ ⎜ ⎟ − ω + ω ⎝ − ω − ω^ ⎠⎝^ − ω +^ ⎠^ ⎝^ − ω − ω^ ⎠ ⎝^ + ⎠
j j
1 2 (^ )
A 1 B
B j j j j j 2 j j
⎛ (^) ω ⎞⎛ ⎞ ⎛ ⎞ ⎜⎜ ⎟⎜⎟ ⎟ =^ +^ ⎜ ⎟ − ω + ω ⎝ − ω − ω^ ⎠⎝^ − ω +^ ⎠^ ⎝^ − ω − ω⎠
0 (^ )
C
j j s 2
Hence, the constant B 1 is:
1
A 1 A 1 A 1
B
j j j 2 2j j 2 2 j j 2
⎛ (^) ω ⎞⎛ ⎞ ⎛ ω ⎞⎛ ⎞ ⎛ − ⎞⎛ ⎞ = (^) ⎜⎜ ⎟⎜⎟ ⎟ = (^) ⎜ ⎟⎜ ⎟ =⎜ ⎟⎜ ⎟ ⎝ − ω − ω^ ⎠⎝^ − ω +^ ⎠^ ⎝^ −^ ω^ ⎠⎝^ − ω +^ ⎠^ ⎝^ ⎠⎝^ − ω + ⎠
Evaluating the transfer function: 1 G(s) s 2
for s = -jω yields:
1 G( j ) j 2
− ω = − ω +
The constant B 1 can be written as:
1
A 1 A
B G
2 j j 2 2 j
⎝ ⎠ ⎝ − ω + ⎠ ⎝ ⎠
( − ωj )
Using the same procedure, B 2 and C are found to be:
2
A 1 A 1 A
B G
j j j 2 2 j j 2 2j
⎛ (^) ω ⎞⎛ ⎞ ⎛ ω⎞⎛ ⎞ ⎛ ⎞ = (^) ⎜⎜ ⎟⎜⎟ ⎟ = (^) ⎜ ⎟⎜ ⎟ =⎜ ⎟ ⎝ ω + ω^ ⎠⎝^ ω +^ ⎠^ ⎝^ ω^ ⎠⎝^ ω + ⎠^ ⎝^ ⎠
( j ω)
2
A
C
⎛ ω ⎞ = ⎜ ⎟ ⎝ +^ ω ⎠
where C is a real number. The partial function expansion is:
j t j t lim e^ −^ ω^ e− ω →∞
Does e− ω∞j^ decay to zero? No. Recall that e jφ^ is the complex exponential unit vector, where the angle of the unit vector is the term in the exponent multiplied by j. The complex
exponential unit vector has a time varying angle ωt. This unit vector rotates about the
origin of its complex plane completing a rotation of 2π radians as t increases by
e− ω^ j^ t 2 t
π ∆ = ω
. The
negative sign is does not indicate decay; it inverts the sign of the angle of the unit vector.
Consequently, the limit does not yield a final value. The limit represents a
unit vector which are accumulated an infinite angle rotating about the origin of a complex plane. However, we cannot distinguish between
j t t lim e− ω →∞
j t t lim e− ω →∞
∞ and ∞ + 2 π. Therefore, there is no final value for
either e j^ ωt^ or e− ωj^ t.
Hence, as t → ∞the steady-state output is:
j t j t 2t Output(t)steady (^) state B e 1 B e 2 Ce − ω ω − − =^ +^ +^0
Substituting in the complex constants B 1 and B 2 :
j t j t steady state
A A
Output(t) G( j )e G( j )e 2 j 2 j
− ω ω −
= − (^) ⎜ ⎟ − ω + (^) ⎜ ⎟ ω ⎝ ⎠ ⎝ ⎠
Because we know that the steady-state response of the system, the particular solution of the system equation for the input, will be a sinusoid since we are forcing the system with a sinusoid, our objective is to eliminate the complex terms and yield a real trigonometric function. We will need to use either Euler’s sine or cosine function:
e j^ e j cos( ) 2
φ (^) + − φ φ =
e j^ e j sin( ) 2 j
φ (^) − − φ φ =
G(jω) is the system’s transfer function G(s) evaluated for s = jω, where ω is the frequency of the forcing function. The relationship between G(jω) and G(-jω) can be seen when both are expressed vectors in the form of their magnitude times a complex exponential unit vector:
1 1
j0 (^) j tan 2 j tan 2 2 2
1 1 e 1 G( j ) e j (^2 ) 4 e
− −
− ⎛⎜^ ⎛⎜^ ω⎞⎟⎞⎟ ⎝ ⎝^ ⎠⎠ ⎛⎜ ⎛⎜ ω⎞⎟⎞⎟ ⎝ ⎝^ ⎠⎠
ω = = = ω + (^) ω + ω +
1 1 1
j0 (^) j tan j tan 2 2 j tan 2 2 2 2
1 1 e 1 1 G( j ) e e j (^2 4 ) 4 e
− − −
− ⎛⎜^ ⎛⎜^ −ω^ ⎞⎟⎞^ ⎟ ⎛⎜ ⎛⎜^ ω⎞⎟ ⎝ ⎝^ ⎠^ ⎠ ⎝ ⎝^ ⎠ ⎛⎜ ⎛⎜ −ω⎞⎟⎞⎟ ⎝ ⎝^ ⎠⎠
− ω = = = = − ω + (^) ω + ω + ω +
⎞⎟ ⎠
G(jω) and G(-jω) have the same magnitude and differ only in the sign of their angle. Let us generalize our notation by defining their magnitude:
2
G( j ) 4
ω ≡ ω +
and angle:
G( j ) N( j ) D( j ) 0 tan 1 tan^1 2 2
φ ≡ ∠ ω = ∠ ω − ∠ ω = − −^ ⎛^ ω^ ⎞^ = − − ⎛^ ω⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠
Using this notation with complex exponential unit vectors:
G( j ω =) G( j ω) e jφ
and
G( − ω =j ) G( j ω) e−^ jφ
We can now rearrange the steady-state output expression into a form which can be simplified using one of Euler’s equations:
j t j t steady state
A A
Output(t) G( j )e G( j )e 2 j 2 j
− ω ω −
= − (^) ⎜ ⎟ − ω + (^) ⎜ ⎟ ω ⎝ ⎠ ⎝ ⎠
j j t j j steady state
A A
Output(t) G( j ) e e G( j ) e e 2 j 2 j
− φ − ω φ ω t −
= − (^) ⎜ ⎟ ω + (^) ⎜ ⎟ ω ⎝ ⎠ ⎝ ⎠
( ) j j t j j t steady state
A
Output(t) G( j ) e e e e 2 j
φ ω − φ − ω −
= (^) ⎜ ⎟ ω − ⎝ ⎠
j( t ) j( t ) steady state
e e Output(t) A G( j ) 2 j
ω +φ − ω +φ −
= ω ⎜ ⎟ ⎝ ⎠
Output(t) (^) steady − state= A G( j ω) sin( ω +t φ)
- Determine the magnitude and phase angle of G(j3).
2 2
2 2
6 j6^6 G( j3) 0. 52 j18 (^52 )
+^ +
G( j3) 6 j6 52 j18 tan 1 6 tan 1 18 0.79 2.81 2.02 rad 6 52
∠ = ∠ + − ∠ − + = −^ ⎛^ ⎞^ − −⎛^ ⎞= − = −
- Evaluate the frequency response equation. The magnitude of the input sine is A = 4.
Output(t) (^) steady − state= A G( j ω) sin( ω +t φ)
Output(t) steady (^) −state ≡ i(t)ss = (4)(0.15)sin(3t −2.02)
Output(t) steady (^) −state ≡ i(t)ss = 0.60sin(3t −2.02)
Alternating current circuit analysis is a frequency response analysis. The input is always a sinusoidally varying voltage. Note that the input voltage is assumed to have
zero phase shift. Often, the output variable of interest is the current drawn by the system. The phase angle φ of the current drawn by a system,
v(t) = V sin( 0 ωt)
i(t) = I sin( 0 ω + φt ) , is measured relative to the
input voltage. Current phase leads or lags are created by capacitive or inductive energy storage within a circuit. For many of our analyses, we will find it convenient to represent the circuit being driven by the source as a single complex impedance load Complex impedances are developed below. They will allow us to work with “phasors”, vectors in a complex plane, as a convenient graphical representation of sinusoidally varying voltages and currents.
ALTERNATING CURRENT
Alternating current (AC) is the worldwide standard for the distribution of electric power. The United States and Canada use a frequency of 60 hertz (cycles/sec). Elsewhere, AC frequency is 50 Hz. When AC current was developed in the United States in the 1890’s, the frequency was 25 Hz. Why we now use 60 Hz and the rest of the world uses 50 Hz is a good question. We will have to use a mix of units for frequency. We will be able to perform some
calculations in Hz but others will require circular frequency with units of
rad sec
. We also mix
units , using both radians and degrees. One number that is useful to keep in mind is 60 Hz = 377 rad sec
The residential service voltage in North America is 110 to 120 VAC. It is a range and does vary with the load on a system and the distance from the electrical distribution line. Typically, the voltage of 115 VAC is assumed in an analysis. The residential voltage elsewhere
in the world ranges from 220 to 240 VAC. Since lower voltage is safer, why is North American voltage lower than elsewhere? Increased current means larger diameter wire and more copper. Copper was cheap in North America when standards were set in the late 1800’s. European standards reflected the higher cost of copper there.
Resistive energy loss during transmission of electric power is a function of the current flow:
2 ELost =R i
Since electrical power , if you increase voltage you may decrease current and deliver the
same power. Consequently, the voltage of AC power is “stepped up” for transmission and “stepped down” for use, decreasing voltage and increasing current. Although it is possible to step up and step down DC voltages of large power flows, it is more expensive. DC electrical energy must be converted to mechanical energy by a DC motor which then drives a DC generator to produce DC electrical power at a different voltage. Paired DC motors and DC generators are expensive to purchase and to operate, since they need maintenance. AC voltages can be stepped up or down using transformers which are far less expensive to build and require little maintenance.
P = vi
We use a various voltages above for industrial motors. Large motors use voltages greater than 110 - 120 VAC for a number of reasons, including economy. The hazard posed by higher voltages is not an issue because large industrial motors are hardwired by electricians. The following are the typical voltages: 208VAC, 230 VAC, 460 VAC, 575 VAC, 2300 VAC. In case you are wondering, an induction motor using 2300 VAC pulls only 49 Amps to produce 200 hp. The same type of motor designed to run at 230 VAC would need 490 Amps, and a lot more copper, to produce 200 hp. Industrial motors also use variable frequency AC current for speed control. AC is supplied to the speed control circuitry at 60 Hz. The AC is converted to a direct current (DC) and then to the needed frequency using circuitry known as an “inverter”.
ROOT-MEAN-SQUARE (RMS) or EFFECTIVE VALUES
In some AC analyses, a single value is used to represent an “average” or “effective” voltage or current. The “effective” value corresponds to the constant, or DC, voltage and current which would deliver the same power. The average value of a sinusoid with no vertical offset, such as v(t) = V sin( 0 ωt)shown below, is zero because of the symmetry of the sine wave.
Expressing it using complex exponentials:
j ( t ) j( t ) 0 0
e e v(t) V cos( t ) V 2
⎛ ω +φ^ + −^ ω +φ ⎞ = ω + φ = (^) ⎜⎜ ⎟⎟ ⎝ ⎠
Those suffering from post-calculus stress syndrome feel free to skip from here to the results below. You are not responsible for the following integration.
T 2 T j( t ) j( t ) 2 RMS 0 0 0 0
1 1 e V V sin( t ) dt V T T 2
⎛ ω +φ^ + −^ ω +φ ⎞ = ω + φ = (^) ⎜⎜ ⎟⎟ ⎝ ⎠
∫ ∫
e dt
( ) ( ) ( )
2 T 2 0 j^ t^ j^ t RMS 0
V
V e e 4T
= ω +φ^ + −^ ω +φ ∫ dt
dt
dt
dt
T
0
∫
Expanding the integral:
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
T 2 T j t j t j2 t j t j t j2 t 0 0
∫ e^ ω +φ^ +^ e^ −^ ω +φ^ dt^ =^ ∫ e^ ω +φ^ +^ 2e^ ω +φ^ e^ −^ ω +φ^ +e−^ ω +φ
( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
T 2 T j t j t j2 t j t j t j2 t 0 0
∫ e^ ω +φ^ +^ e^ −^ ω +φ^ dt^ =^ ∫ e^ ω +φ^ +^ 2e^ ω +φ^ e^ −^ ω +φ^ +e−^ ω +φ
( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
T T j2 t j t j t j2 t j2 t 0 j2 t 0 0
∫ e^ ω +φ^ +^ 2e^ ω +φ^ e^ −^ ω +φ^ +^ e^ −^ ω +φ^ dt^ =^ ∫ e^ ω +φ^ +^ 2e^ +e−^ ω +φ
( ) ( ) ( )
( ) ( )
T T T j2 t 0 j2 t j2 t j2 t 0 0 0 0
∫ e^ ω +φ^ +^ 2e^ +^ e^ −^ ω +φ^ dt^ =^ ∫ e^ ω +φ^ dt^ +^ ∫e^ −^ ω +φdt^ + 2e dt
Evaluating the first integral term using
u eu du^ de dx dx
= and recognizing that the circular frequency
2 T
π ω =
( ) ( )
T (^) j2 2 t j2 2 T j2 2 0 T T T j 4^2 j 0
T T
e dt e e e e 4 4
⎛⎜ π^ +φ ⎞⎟ ⎛⎜ π^ +φ ⎞⎟ ⎛⎜ π+φ⎞⎟ ⎝ ⎠ (^) = ⎛⎜^ ⎝ ⎠ (^) − ⎝ ⎠⎞⎟= π+^ φ^ φ π ⎜^ ⎟ π ⎝ ⎠
∫ −
Complex exponentials are vectors! The complex exponentials e j 4(^ π+^2 φ)^ and^ are the same vector since 0, 2π, 4 π, and any other integer multiple of 2π, are the same angle. Therefore:
e j2φ
( ) ( ) (^ )
T (^) j2 2 t T j 4^2 j2 j2 j 0
T T
e dt e e e e 4 4
⎛⎜ π+φ⎞⎟ ⎝ ⎠ (^) = π+^ φ^ − φ^ = φ^ − φ ∫ (^) π π
and
( ) ( ) (^ )
T (^) j2 2 t T j 4^2 j2^ j2^ j 0
T T
e dt e e e e 4 4
− ⎛⎜^ π+φ⎞⎟ ⎝ ⎠ (^) = −^ π+^ φ^ − −^ φ^ = −^ φ^ − −^ φ ∫ (^) π π
leaving the only term in the integral to be:
( ) ( ) ( ) (^ )
T T j2 t 0 j2 t 0 0 0
∫ e^ ω +φ^ +^ 2e^ +^ e^ −^ ω +φ dt^ =^ ∫2e dt^ =^ 2 T^ −^0 =2T
Hence:
( ) ( ) ( ) (^ )
2 T 2 2 0 j^ t^ j^ t 0 RMS 0
V V
V e e dt 2T 4T 4T (^2 )
= ω +φ^ + −^ ω +φ = = ∫
2 V (^0) =V 0
Here is the result. The effective or root-mean-square (RMS) value of
is:
v(t) = V sin( 0 ωt)
0 RMS 0
V
V 0.707 V
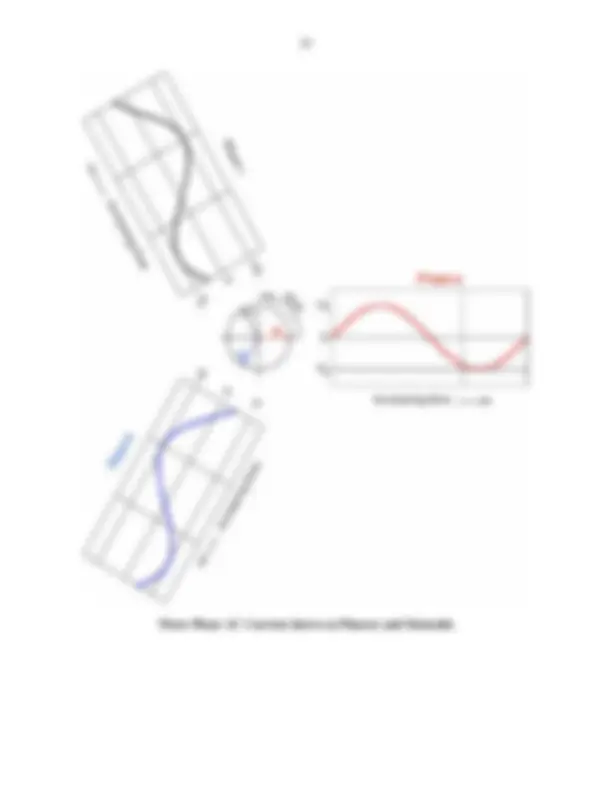
The figure below shows three phase 120 VAC sine waves, where VAC is the root-mean-
squared (RMS) voltage. The peak voltage is (^) ( 2 )(120 VAC )= 170 volts. Unfortunately, it is
often difficult to visualize the relationship between trigonometric functions. For example, consider the signals a(t), b(t) and c(t) below. Assume the phase angle φ of a(t) is zero:
a(t) = V sin( 0 ωt)
Do signals b(t) and c(t) have positive or negative phase angles φb and φ (^) c?
It is impossible to tell the sign of a phase angle a steady-state, time domain plot of two or more sinusoids. Signal b(t) could “lag” a(t) by 120o^ or “lead” a(t) 240o. Likewise, c(t) could “lag” a(t) by 240o^ or “lead” a(t) 120o. When we work with three phase alternating current, we will assume that voltage a(t) has a phase angle of zero, b(t) lags a(t) 120o^ by and AC voltage c(t) lag a(t) by 240o:
o b(t) = V sin( 0 ω −t 120 )
o c(t) = V sin( 0 ω −t 240 )
IMPORTANT: We conventionally mix angular units when working with AC. We MUST use
[ ]
rad sec
ω ≡ and [ φ ≡] rad when we evaluate these expressions. However, the phase angle φ is
usually expressed in degrees when we report our results, since degrees are easier to visualize than are radians.
Algebraic expressions of these trigonometric functions can also be difficult to visualize. For example, consider the voltages created by the differences a(t)-b(t), b(t)-c(t), and c(t)-a(t)?
o a(t) − b(t) = V 0 ⎡⎣sin(^ ωt) − sin( ω −t 120 )⎤⎦
o o b(t) − c(t) = V 0 ⎡⎣sin(^ ω −t 120 ) − sin( ω −t 240 )⎤⎦
o c(t) − a(t) = V 0 ⎡⎣sin( ωt) − sin( ω −t 240 )⎤⎦
The algebraic sum of two sinusoids with the same frequency will be a sinusoid at that frequency. What are the magnitudes and phase shifts relative to a(t), b(t), and c(t)?
The magnitude of a(t)-b(t), b(t)-c(t), and c(t)-a(t) may be a surprise. It is a common error to presume that the amplitude of is V 0 , but comparing the plots of a(t) and a(t)-b(t) we see that the amplitude of a(t)-b(t) is greater. Do you remember the trigonometric formulae you learned in high school but never used? No one does, but now is when you could finally use them. However, with apologies to your high school math teacher, it is easier to find the magnitude
as a vector construction using complex exponential unit vectors and
Euler’s sine formula than it would be to use trigonometric formulae.
sin( ωt) − sin( ω −t 120 )^ o
We wish to determine the magnitude of a(t) – b(t). The first step is to create complex exponentials which represent a(t) and b(t). The vectors must have the correct amplitude and phase angle φ. Since we are evaluating steady-state relationships that must hold for any arbitrary time t, we are free to choose the time t at which we will draw the vector diagrams. The most convenient time is t = 0. Phase a(t) has a phase angle of zero, so it plots on the positive real axis. Positive angles are counter-clockwise. Phase b(t) has a negative phase angle since it peaks later in time than does a(t).
Now the hard part. We need to find the magnitude and phase angle of a(0) – b(0). We know the lengths of two of the sides of the triangle formed by a(0), b(0), and a(0) – b(0) and we know the angle between a(0) and b(0). There is surely a sophisticated formula which we could hunt for in a math handbook, that would yield magnitude and phase angle of a(0) – b(0), but it is usually faster to use what we know then search for what we may not be able to find. We can create a right triangle with a(0) – b(0) as its hypotenuse using simple trig.
The Pythagorean theorem is used to calculated the magnitude of the vector a(0) –b(0):
( ( (^ ))) ( (^ ))
o 2 o^2 a(0) − b(0) = V 0 1 + cos 60 + V sin 60 0
JJJJJJJJJJJJG
Factoring V 0 out of the radical
(^2) o 2 o^2 a(0) b(0) V 0 1 cos 60 sin 60 − = ⎡^ + + ⎤ ⎢⎣ ⎥⎦
JJJJJJJJJJJJG
( ( )) ( ( )) o 2 o^2 a(0) − b(0) = V 0 1 + cos 60 + sin 60
JJJJJJJJJJJJG
Expanding the first term in the radical:
( (^ )) (^ )^ (^ )
o 2 o 1 + cos 60 = 1 + 2 cos 60 + cos 2 60 o
Rearranging:
( ) ( ) ( ) o 2 o 2 o a(0) − b(0) = V 0 1 + 2cos 60 + ⎡⎣cos^60 +sin 60 ⎤⎦
JJJJJJJJJJJJG
Using the trigonometric relationship from a unit circle: cos 2 ( α ) + sin 2 ( α )= 1
( ) o a(0) − b(0) = V 0 1 + 2 cos 60 + 1
JJJJJJJJJJJJG
Yields the result
a(0) − b(0) =V 0 3
JJJJJJJJJJJJG
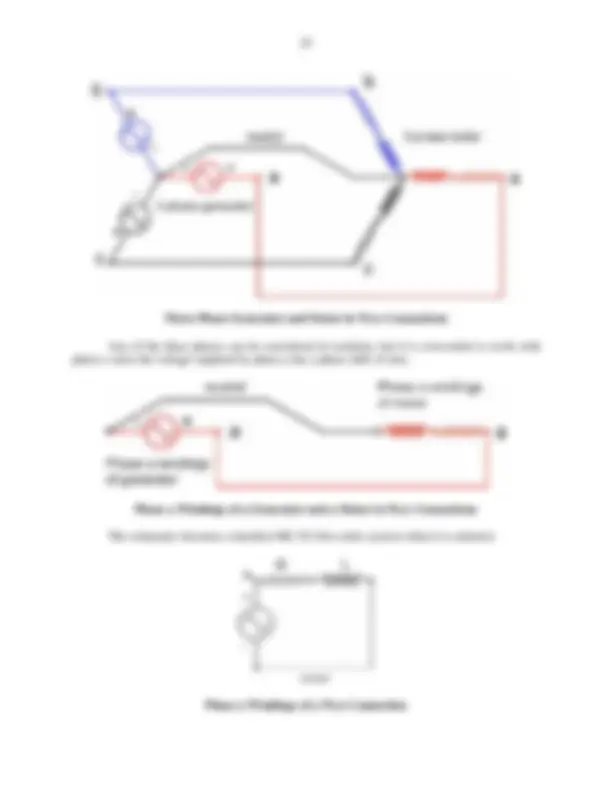
Line-to-Line Voltage
This is a useful relationship to remember. The “line to line” voltage (in this case a(t)-
b(t)) in a three phase machine is 3 times the voltage of a single phase relative to the reference voltage “neutral” with ground potential.
Returning to the time domain plots, note that it is difficult to visualize the phase angle of a(t)-b(t) relative to a(t) from these plots. Also note that the phase angles of the signals a(t)-b(t), b(t)-c(t), and c(t)-a(t) differ from each other and from a(t), b(t), and c(t). The phase angle of a(0)-b(0) relative to a(0) is easily derived from the vector construction from trigonometry:
