Docsity
Log inSign up
Docsity
Prepare for your exams
Prepare for your exams

Study with the several resources on Docsity

Earn points to download
Earn points to download

Earn points by helping other students or get them with a premium plan

Guidelines and tips
Guidelines and tips
Sell on Docsity
Sell on Docsity
Log inSign up

Prepare for your exams

Study with the several resources on Docsity

Find documents

Prepare for your exams with the study notes shared by other students like you on Docsity

Search Store documents

The best documents sold by students who completed their studies

Search through all study resources
Docsity AINEW

Summarize your documents, ask them questions, convert them into quizzes and concept maps

Explore questions

Clear up your doubts by reading the answers to questions asked by your fellow students

Earn points to download

Earn points by helping other students or get them with a premium plan

Share documents
download point icon20 Points

For each uploaded document

Answer questions
download point icon5 Points

For each given answer (max 1 per day)

All the ways to get free points
Get points immediately

Choose a premium plan with all the points you need

Study Opportunities

Choose your next study program

Get in touch with the best universities in the world. Search through thousands of universities and official partners

Community

Ask the community

Ask the community for help and clear up your study doubts

University Rankings

Discover the best universities in your country according to Docsity users

Free resources

Our save-the-student-ebooks!

Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors

From our blog

Exams and Study
Go to the blog

Understanding Period and Amplitude in Trigonometric Graphs, Schemes and Mind Maps of Physics

University of Northern Iowa (UNI)Physics

The concepts of period and amplitude in trigonometric graphs, using examples of sin and cos functions. It covers the rules for transforming trig graphs and provides exercises for practice.

Typology: Schemes and Mind Maps

2021/2022

Uploaded on 09/27/2022

anjushri
anjushri 🇺🇸

4.8

(14)

243 documents

1 / 11

Toggle sidebar

This page cannot be seen from the preview

Don't miss anything!

bg1
Amplitude and Period for
Graphs
1.
pf3
pf4
pf5
pf8
pf9
pfa

Partial preview of the text

Download Understanding Period and Amplitude in Trigonometric Graphs and more Schemes and Mind Maps Physics in PDF only on Docsity!

Amplitude and Period for

Graphs

Period and Amplitude A graph which consists of the same basic pattern repeated over and over is called periodic. The period is the horizontal coverage of the basic pattern. The amplitude of a graph is half of its vertical coverage. y = sin x 360

Period Amplitude

Heinemann, p.53, EX 4A (ORALLY)

Graphing trig functions Recall the rules for transforming graphs. The same rules apply for trig graphs:

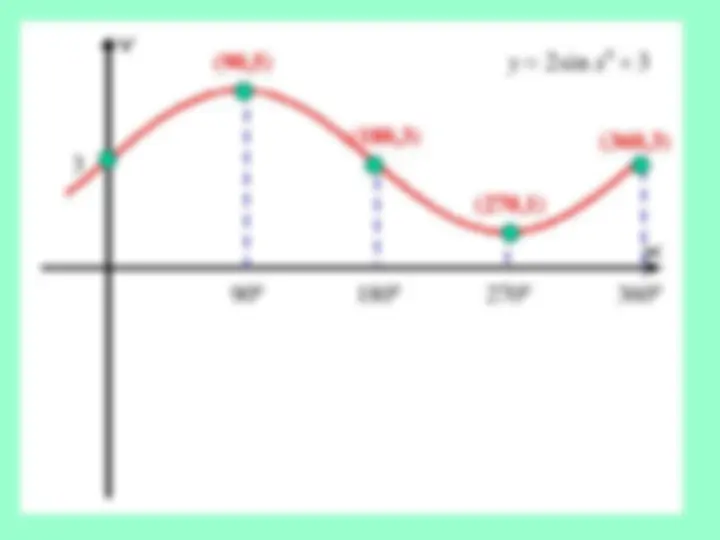
Example 1 Sketch and annotate the graph of 0

y = 2sin x + 3

Solution: Graphing trig functions

  1. Amplitude = 2 so vertical extent = 4
  2. b = 1 so period = 360 0
  3. Normally sin x graph starts at 0, so this graph starts at +3. 0  x  360

0

y = 2sin x + 3

0 180 0

0

0

  1. Amplitude = 2 so vertical extent = 4
  2. b = 1 so period = 360 0
  3. Normally sin x graph starts at 0, so this graph starts at +3.

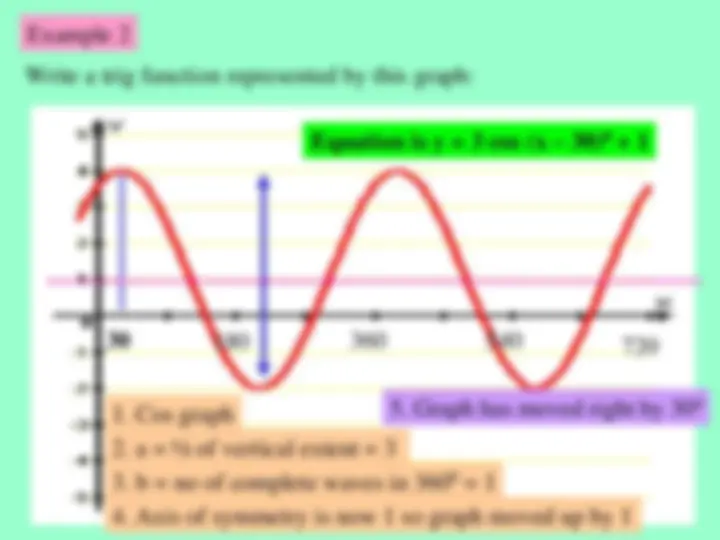
Example 2 Write a trig function represented by this graph: (^30) 180 360 540 720

  1. Cos graph
  2. a = ½ of vertical extent = 3
  3. b = no of complete waves in 360 0 = 1
  4. Axis of symmetry is now 1 so graph moved up by 1
    1. Graph has moved right by 30 0 **Equation is y = 3 cos (x – 30) 0
  • 1**

Heinemann, p.54, EX 4B Q1 & Q