All about data structure with c language, Study notes of Data Structures and Algorithms

Download All about data structure with c language and more Study notes Data Structures and Algorithms in PDF only on Docsity!

DATA STRUCTURES USING

“C”

DATA STRUCTURES USING

“C”

LECTURE NOTES

Prepared by

Dr. Subasish Mohapatra

Department of Computer Science and Application

College of Engineering and Technology, Bhubaneswar

Biju Patnaik University of Technology, Odisha

CONTENTS Lecture- 01 Introduction to Data structure Lecture- 02 Search Operation Lecture- 03 Sparse Matrix and its representations Lecture- 04 Stack Lecture- 05 Stack Applications Lecture- 06 Queue Lecture- 07 Linked List Lecture- 08 Polynomial List Lecture- 09 Doubly Linked List Lecture- 10 Circular Linked List Lecture- 11 Memory Allocation Lecture- 12 Infix to Postfix Conversion Lecture- 13 Binary Tree Lecture- 14 Special Forms of Binary Trees Lecture- 15 Tree Traversal Lecture- 16 AVL Trees Lecture- 17 B+-tree Lecture- 18 Binary Search Tree (BST) Lecture- 19 Graphs Terminology Lecture- 20 Depth First Search Lecture- 21 Breadth First Search Lecture- 22 Graph representation Lecture- 23 Topological Sorting Lecture- 24 Bubble Sort Lecture- 25 Insertion Sort Lecture- 26 Selection Sort Lecture- 27 Merge Sort Lecture- 28 Quick sort Lecture- 29 Heap Sort Lecture- 30 Radix Sort Lecture- 31 Binary Search Lecture- 32 Hashing Lecture- 33 Hashing Functions

Module- 1 Lecture- 01 Introduction to Data structures In computer terms, a data structure is a Specific way to store and organize data in a computer's memory so that these data can be used efficiently later. Data may be arranged in many different ways such as the logical or mathematical model for a particular organization of data is termed as a data structure. The variety of a particular data model depends on the two factors -  Firstly, it must be loaded enough in structure to reflect the actual relationships of the data with the real world object.  Secondly, the formation should be simple enough so that anyone can efficiently process the data each time it is necessary. Categories of Data Structure: The data structure can be sub divided into major types:  Linear Data Structure  Non-linear Data Structure Linear Data Structure: A data structure is said to be linear if its elements combine to form any specific order. There are basically two techniques of representing such linear structure within memory.  First way is to provide the linear relationships among all the elements represented by means of linear memory location. These linear structures are termed as arrays.  The second technique is to provide the linear relationship among all the elements represented by using the concept of pointers or links. These linear structures are termed as linked lists. The common examples of linear data structure are:  Arrays  Queues  Stacks  Linked lists Non linear Data Structure: This structure is mostly used for representing data that contains a hierarchical relationship among various elements. Examples of Non Linear Data Structures are listed below:  Graphs  family of trees and  table of contents Tree: In this case, data often contain a hierarchical relationship among various elements. The data structure that reflects this relationship is termed as rooted tree graph or a tree.

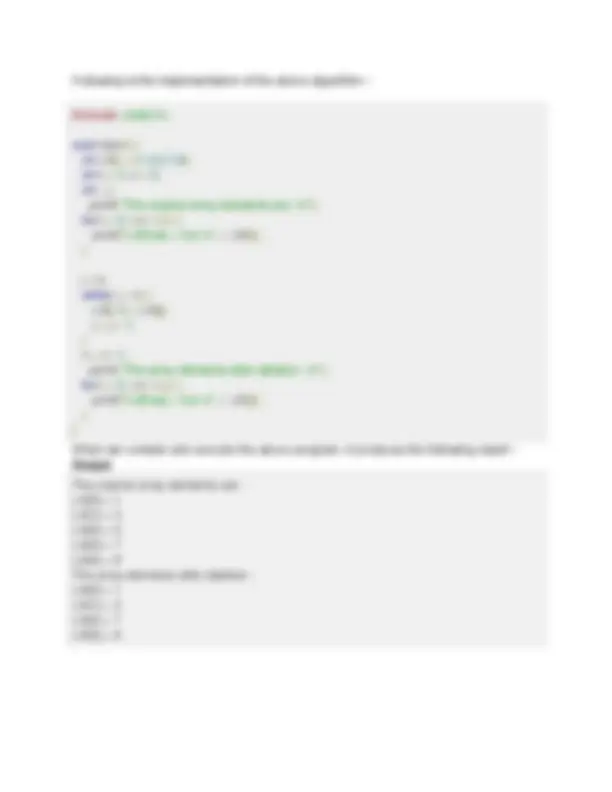
char 0 int 0 float 0. double 0.0f void wchar_t 0 Insertion Operation Insert operation is to insert one or more data elements into an array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array. Here, we see a practical implementation of insertion operation, where we add data at the end of the array − Algorithm Let LA be a Linear Array (unordered) with N elements and K is a positive integer such that K<=N. Following is the algorithm where ITEM is inserted into the Kth^ position of LA −

1. Start
2. Set J = N
3. Set N = N+
4. Repeat steps 5 and 6 while J >= K
5. Set LA[J+1] = LA[J]
6. Set J = J- 1
7. Set LA[K] = ITEM
8. Stop Example Following is the implementation of the above algorithm − Live Demo #include <stdio.h> main() { int LA[] = { 1 , 3 , 5 , 7 , 8 }; int item = 10 , k = 3 , n = 5 ; int i = 0 , j = n; printf("The original array elements are :\n"); for(i = 0 ; i<n; i++) { printf("LA[%d] = %d \n", i, LA[i]); }

n = n + 1 ; while( j >= k) { LA[j+ 1 ] = LA[j]; j = j - 1 ; } LA[k] = item; printf("The array elements after insertion :\n"); for(i = 0 ; i<n; i++) { printf("LA[%d] = %d \n", i, LA[i]); } } When we compile and execute the above program, it produces the following result − Output The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after insertion : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 10 LA[4] = 7 LA[5] = 8 Deletion Operation Deletion refers to removing an existing element from the array and re-organizing all elements of an array. Algorithm Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the Kth^ position of LA.

1. Start
2. Set J = K
3. Repeat steps 4 and 5 while J < N
4. Set LA[J] = LA[J + 1]
5. Set J = J+
6. Set N = N- 1
7. Stop Example

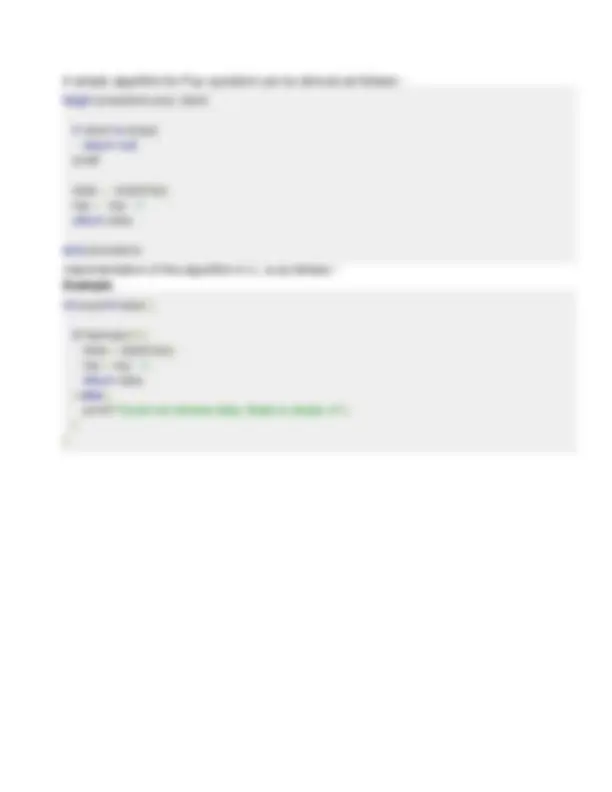
Lecture- 02 Search Operation You can perform a search for an array element based on its value or its index. Algorithm Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to find an element with a value of ITEM using sequential search.

1. Start
2. Set J = 0
3. Repeat steps 4 and 5 while J < N
4. IF LA[J] is equal ITEM THEN GOTO STEP 6
5. Set J = J +
6. PRINT J, ITEM
7. Stop Example Following is the implementation of the above algorithm − Live Demo #include <stdio.h> void main() { int LA[] = { 1 , 3 , 5 , 7 , 8 }; int item = 5 , n = 5 ; int i = 0 , j = 0 ; printf("The original array elements are :\n"); for(i = 0 ; i<n; i++) { printf("LA[%d] = %d \n", i, LA[i]); } while( j < n){ if( LA[j] == item ) { break; } j = j + 1 ; } printf("Found element %d at position %d\n", item, j+ 1 ); } When we compile and execute the above program, it produces the following result − Output The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5

LA[3] = 7

LA[4] = 8

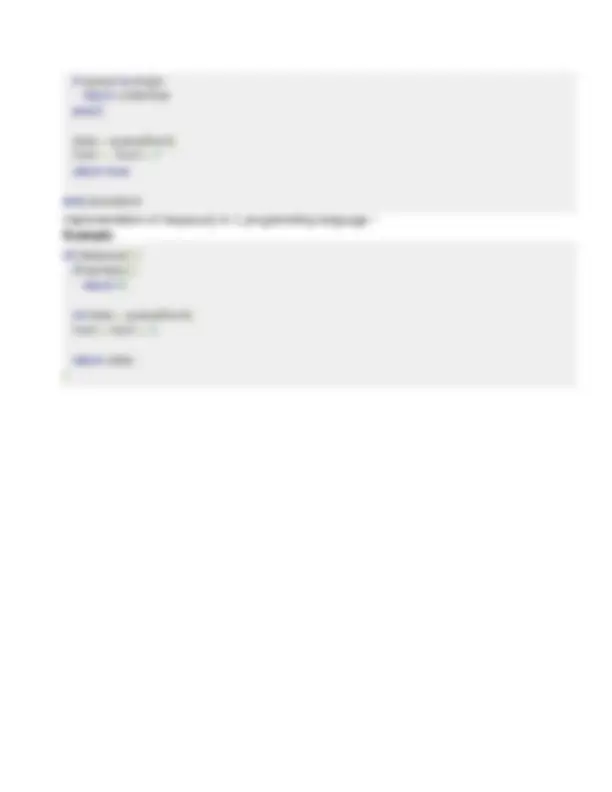
Found element 5 at position 3 Update Operation Update operation refers to updating an existing element from the array at a given index. Algorithm Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to update an element available at the Kth^ position of LA.

1. Start
2. Set LA[K-1] = ITEM
3. Stop Example Following is the implementation of the above algorithm − Live Demo #include <stdio.h> void main() { int LA[] = { 1 , 3 , 5 , 7 , 8 }; int k = 3 , n = 5 , item = 10 ; int i, j; printf("The original array elements are :\n"); for(i = 0 ; i<n; i++) { printf("LA[%d] = %d \n", i, LA[i]); } LA[k- 1 ] = item; printf("The array elements after updation :\n"); for(i = 0 ; i<n; i++) { printf("LA[%d] = %d \n", i, LA[i]); } } When we compile and execute the above program, it produces the following result − Output The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8

Lecture- 03 Sparse Matrix and its representations A matrix is a two-dimensional data object made of m rows and n columns, therefore having total m x n values. If most of the elements of the matrix have 0 value , then it is called a sparse matrix. Why to use Sparse Matrix instead of simple matrix?  Storage: There are lesser non-zero elements than zeros and thus lesser memory can be used to store only those elements.  Computing time: Computing time can be saved by logically designing a data structure traversing only non-zero elements.. Example: 0 0 3 0 4 0 0 5 7 0 0 0 0 0 0 0 2 6 0 0 Representing a sparse matrix by a 2D array leads to wastage of lots of memory as zeroes in the matrix are of no use in most of the cases. So, instead of storing zeroes with non-zero elements, we only store non-zero elements. This means storing non-zero elements with triples- (Row, Column, value). Sparse Matrix Representations can be done in many ways following are two common representations:

1. Array representation
2. Linked list representation Method 1: Using Arrays #include<stdio.h> int main() { // Assume 4x5 sparse matrix int sparseMatrix[4][5] = { {0 , 0 , 3 , 0 , 4 }, {0 , 0 , 5 , 7 , 0 }, {0 , 0 , 0 , 0 , 0 }, {0 , 2 , 6 , 0 , 0 } }; int size = 0; for (int i = 0; i < 4; i++) for (int j = 0; j < 5; j++) if (sparseMatrix[i][j] != 0) size++; int compactMatrix[3][size]; // Making of new matrix

int k = 0; for (int i = 0; i < 4; i++) for (int j = 0; j < 5; j++) if (sparseMatrix[i][j] != 0) { compactMatrix[0][k] = i; compactMatrix[1][k] = j; compactMatrix[2][k] = sparseMatrix[i][j]; k++; } for (int i=0; i<3; i++) { for (int j=0; j<size; j++) printf("%d ", compactMatrix[i][j]); printf("\n"); } return 0; }

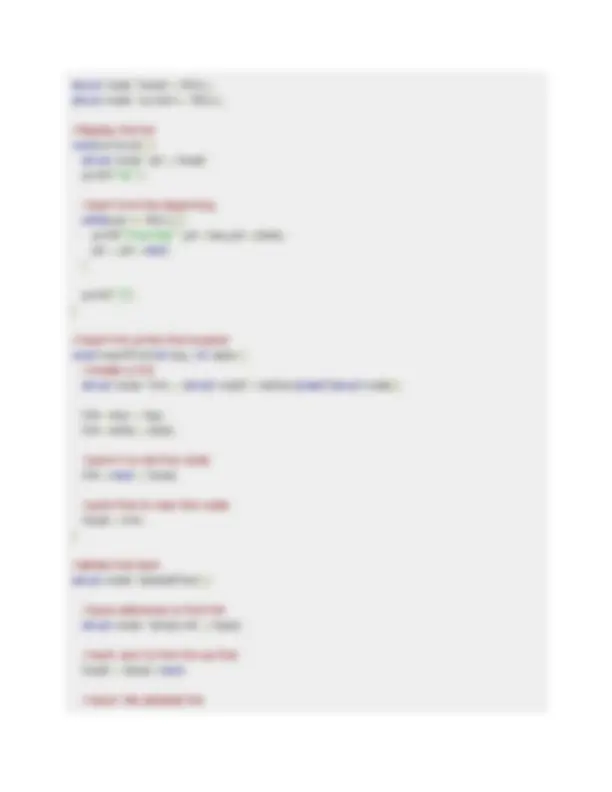
 pop() − Removing (accessing) an element from the stack. When data is PUSHed onto stack. To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks −  peek() − get the top data element of the stack, without removing it.  isFull() − check if stack is full.  isEmpty() − check if stack is empty. At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it. First we should learn about procedures to support stack functions − peek() Algorithm of peek() function − begin procedure peek return stack[top] end procedure Implementation of peek() function in C programming language − Example int peek() { return stack[top]; } isfull() Algorithm of isfull() function − begin procedure isfull if top equals to MAXSIZE return true else return false endif end procedure Implementation of isfull() function in C programming language − Example bool isfull() { if(top == MAXSIZE) return true; else return false; }

isempty() Algorithm of isempty() function − begin procedure isempty if top less than 1 return true else return false endif end procedure Implementation of isempty() function in C programming language is slightly different. We initialize top at - 1, as the index in array starts from 0. So we check if the top is below zero or - 1 to determine if the stack is empty. Here's the code − Example bool isempty() { if(top == - 1 ) return true; else return false; } Push Operation The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −  Step 1 − Checks if the stack is full.  Step 2 − If the stack is full, produces an error and exit.  Step 3 − If the stack is not full, increments top to point next empty space.  Step 4 − Adds data element to the stack location, where top is pointing.  Step 5 − Returns success. If the linked list is used to implement the stack, then in step 3, we need to allocate space dynamically. Algorithm for PUSH Operation A simple algorithm for Push operation can be derived as follows − begin procedure push: stack, data if stack is full

A simple algorithm for Pop operation can be derived as follows − begin procedure pop: stack if stack is empty return null endif data ← stack[top] top ← top - 1 return data end procedure Implementation of this algorithm in C, is as follows − Example int pop(int data) { if(!isempty()) { data = stack[top]; top = top - 1 ; return data; } else { printf("Could not retrieve data, Stack is empty.\n"); } }

Lecture- 05 Stack Applications Three applications of stacks are presented here. These examples are central to many activities that a computer must do and deserve time spent with them.

1. Expression evaluation
2. Backtracking (game playing, finding paths, exhaustive searching)
3. Memory management, run-time environment for nested language features. Expression evaluation In particular we will consider arithmetic expressions. Understand that there are boolean and logical expressions that can be evaluated in the same way. Control structures can also be treated similarly in a compiler. This study of arithmetic expression evaluation is an example of problem solving where you solve a simpler problem and then transform the actual problem to the simpler one. Aside: The NP-Complete problem. There are a set of apparently intractable problems: finding the shortest route in a graph (Traveling Salesman Problem), bin packing, linear programming, etc. that are similar enough that if a polynomial solution is ever found (exponential solutions abound) for one of these problems, then the solution can be applied to all problems. Infix, Prefix and Postfix Notation We are accustomed to write arithmetic expressions with the operation between the two operands: a+b or c/d. If we write a+b*c, however, we have to apply precedence rules to avoid the ambiguous evaluation (add first or multiply first?). There's no real reason to put the operation between the variables or values. They can just as well precede or follow the operands. You should note the advantage of prefix and postfix: the need for precedence rules and parentheses are eliminated. Infix Prefix Postfix a + b + a b a b + a + b * c + a * b c a b c * + (a + b) * (c - d) * + a b - c d a b + c d - * b * b - 4 * a * c 40 - 3 * 5 + 1 Postfix expressions are easily evaluated with the aid of a stack. Infix, Prefix and Postfix Notation KEY Infix Prefix Postfix a + b + a b a b +