Chapter 3. Section 1
Page 1
Section 3.1 – Addition and Subtraction
Homework (pages 104-105) problems 1-5
Addition of Whole Numbers:
• Recall the notation n(A) means the number of elements in the set A
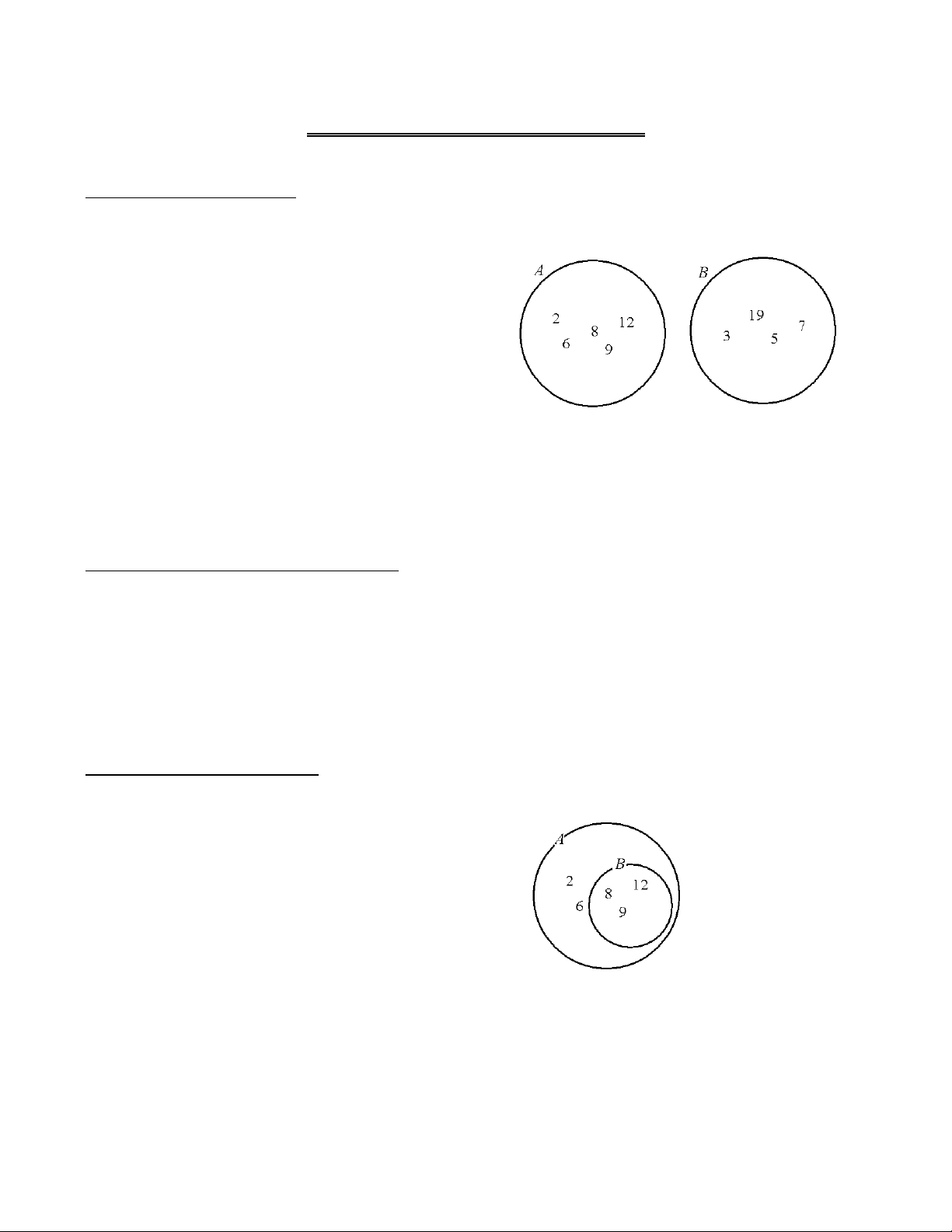
• Formal definition of addition of whole numbers : If AB
∩=∅
, the whole number a = n(A) and the
whole number b = n(B), the a + b = n(
AB
∪
)
• Example
AB
∩=∅
, n(A) = 5 and n(B) = 4
n(
AB
∪
) = 9
• Why is it necessary for us to specify that A and B are disjoint?
• Why is it necessary for a and b to be whole numbers?
• We can also think of addition on the number line, where a + b is found by marking a on the number
line, and then moving over b units (again, a and b are whole numbers)
Properties of Addition of Whole Numbers:
• Closure à the sum of any two whole numbers is a whole number
• Example, page 104 number 3a and 3j. Are the sets closed under addition
{0,10,20,30…} Yes
A = {x | x is a whole number less than 17} No.
10,12 but (1210)22A
AA
∈∈+=∉
• Commutative à a + b = b + a
• Associative à (a + b) + c = a + (b + c)
• Identity à a + 0 = 0 + a = a
Subtraction of Whole Numbers:
• Formal definition of subtraction of whole numbers: If
BA
⊆
, the whole number a = n(A) and the
whole number b = n(B), the a – b = n(
AB
−
)
• Example
BA
⊆
. n(A) = 5, and n(B) = 3
n(A – B) = 2
• Subtraction using the missing-addend approach. This is the equivalent of saying what plus 8 is
equal to 12? If the addition facts are clearly understood, this would result in an answer of 4
i.e. a + 8 = 12. a = 4
This is equivalent to 12 – 8 = 4
