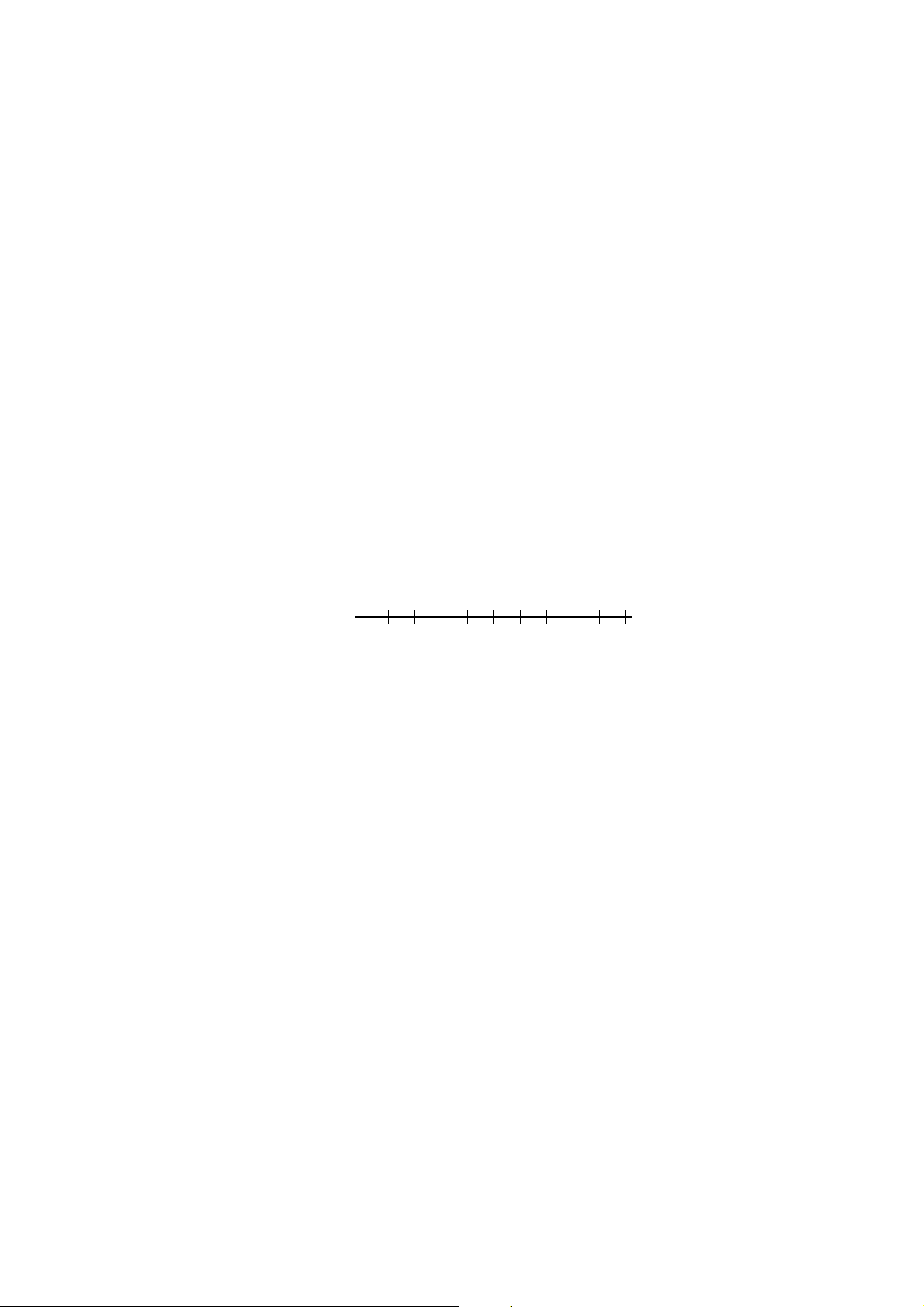



Study with the several resources on Docsity

Earn points by helping other students or get them with a premium plan


Prepare for your exams
Study with the several resources on Docsity

Earn points to download
Earn points by helping other students or get them with a premium plan
Community
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
Material Type: Quiz; Class: Intermediate Algebra; Subject: Mathematics; University: Utica College; Term: Spring 2005;
Typology: Quizzes
1 / 2

This page cannot be seen from the preview
Don't miss anything!
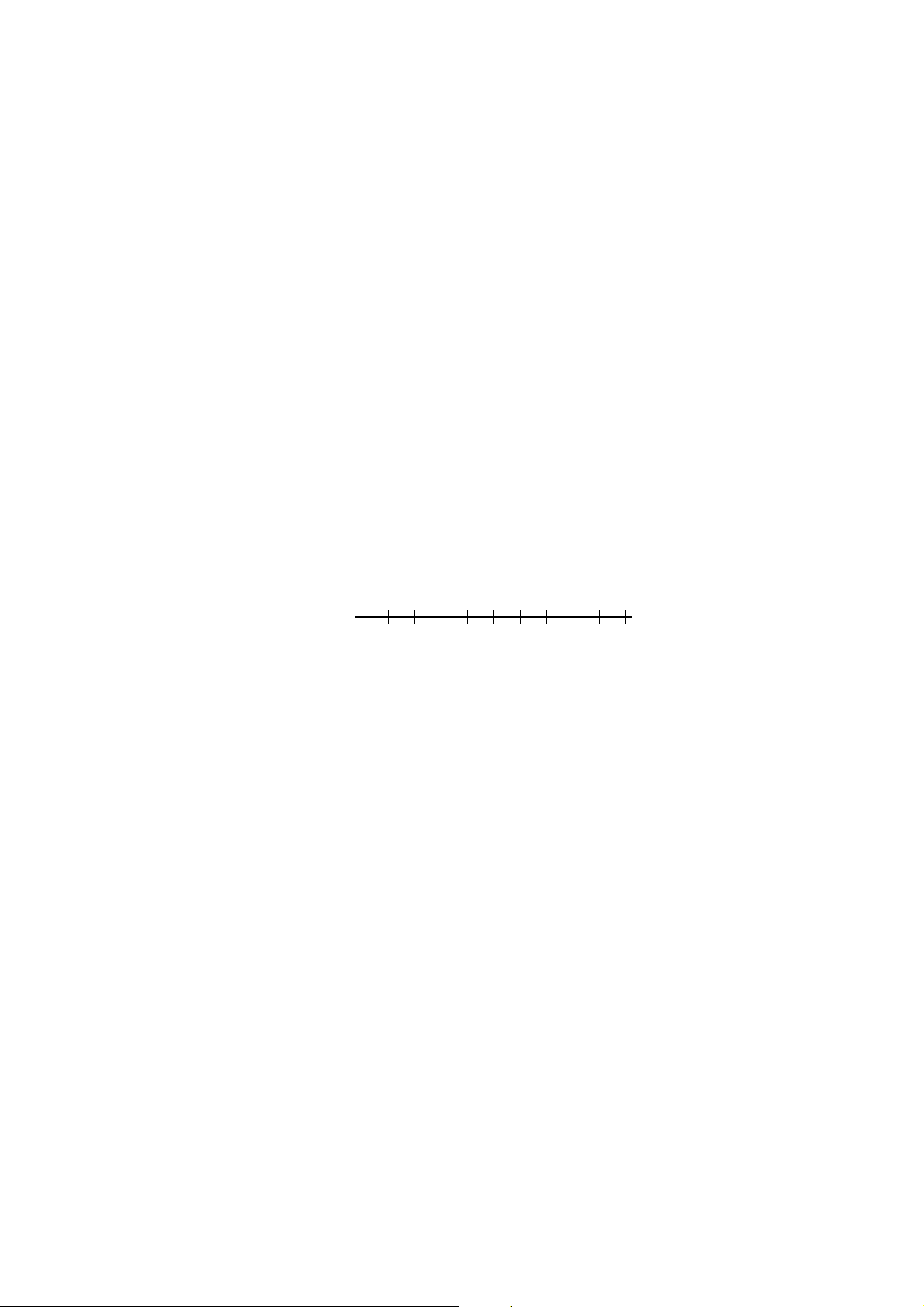

Friday, February 11, 2005
3 − x ≥ 7 − 3 x =⇒ 3 + 2x ≥ 7 =⇒ 2 x ≥ 4 =⇒ x ≥ 2
So the solution set is {x | x ≥ 2 }
(b) Write your answer in interval notation.
(c) Indicate your solution on the number line below.
| 2 x + 3| ≥ 3
First split this as two inequalities. Remember, this is saying that we want the expression (2x + 3) to live at least 3 units away from 0. To be that far from zero, the expression can be to the right of 3 (greater than or equal to 3), or to the left of -3 (less than or equal to -3). So we have
2 x + 3 ≥ 3 or 2x + 3 ≤ − 3
Solving each of these inequalities individually, we get
x ≥ 0 or x ≤ − 3
(a) f (2) = (2)^2 + 2 − 3 = 4 + 2 − 3 = 3 (b) f (−1) = (−1)^2 + (−1) − 3 = 1 − 1 − 3 = − 3 (c) f (a) = a^2 + a − 3