Calculus I, Section 4.3, #14
Maximum and Minimum Values
For the function1
f(x) = cos2(x)−2 sin (x),0≤x≤2π
(a) Find the intervals on which fis increasing or decreasing.
We need to find the intervals where f′is positive and where f′is negative.
f′(x) = 2 cos (x)· − sin (x)−2 cos (x)
=−2 cos (x) (sin (x) + 1)
The critical numbers are the solutions to
0 = −2 cos (x) (sin (x) + 1)
so
0 = cos (x) or 0 = sin (x) + 1
x=π
2,3π
2or x=3π
2
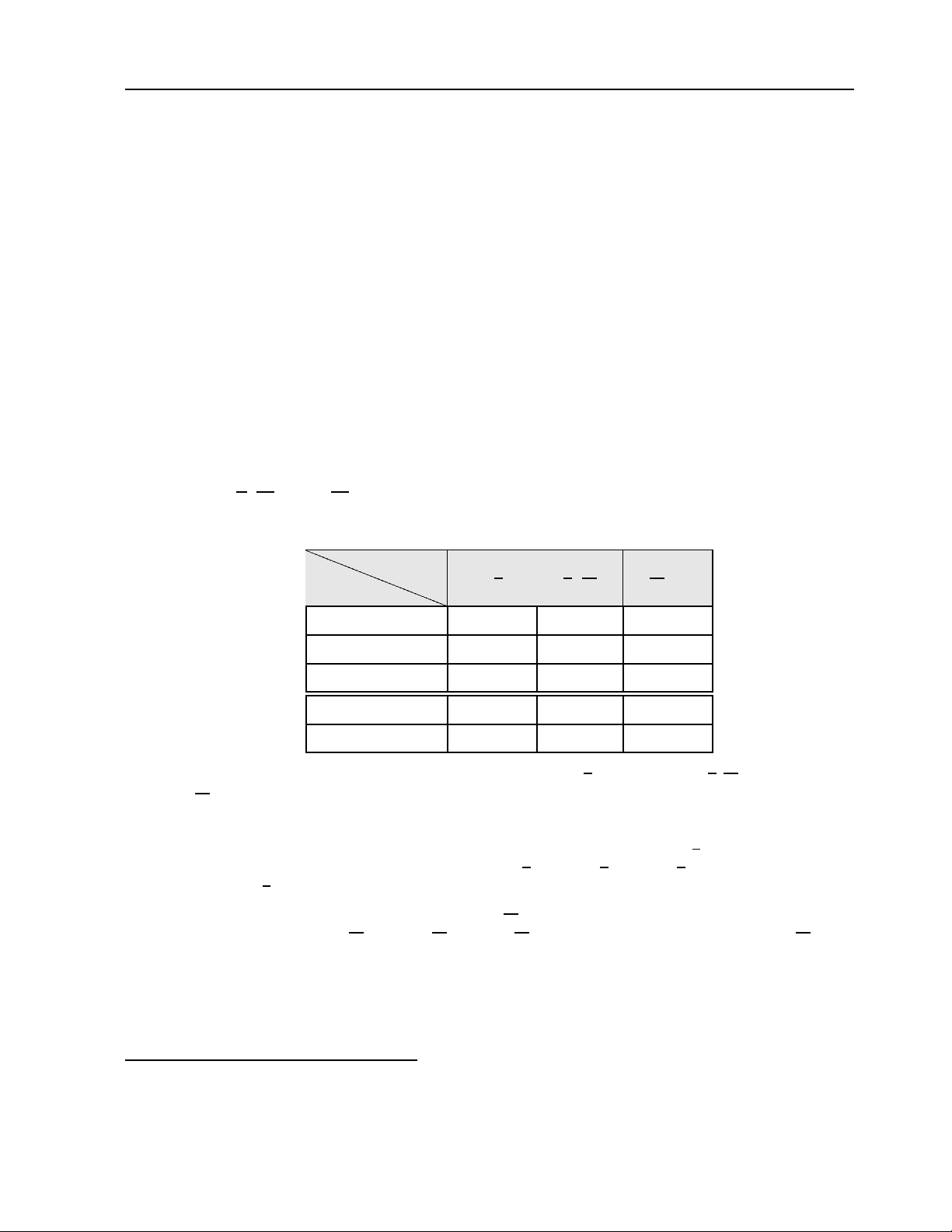
Now we’ll analyze the signs of the factors of f′on the interval 0 ≤x≤2π.2
Factor
Interval 0,π
2π
2,3π
23π
2,2π
−2−−−
cos (x) + −+
sin (x) + 1 + + +
f′(x)−+−
fdecreasing increasing decreasing
Thus the function f(x) = cos2(x)−2 sin (x) is decreasing on 0,π
2, increasing on π
2,3π
2, and decreasing
on 3π
2,2π.
(b) Find the local maximum and minimum values of f.
From the table above, note that the derivative changes sign from −to + at x=π
2, so by First Derivative
Test (FDT) the function has a local minimum of fπ
2= cos2π
2−2 sin π
2= 02−2·1 = −2 that
occurs at x=π
2.
The derivative changes sign from + to −at x=3π
2, so by First Derivative Test (FDT) the function
has a local maximum of f3π
2= cos23π
2−2 sin 3π
2= 02−2· −1 = 2 that occurs at x=3π
2.
1Stewart, Calculus, Early Transcendentals, p. 301, #14.
2Some teachers prefer that their students use a table and analyze the behavior of the factors of f′to determine the sign of
f′, whereas others have their students test values in the intervals to determine the sign of f′. In the l ong-run, its probably best
to understand how to analyze the factors, but be sure you know what your teacher wants you to do.
Continued =⇒
